Défi [niveau 3ème - 2de - 2de +]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 22 Juil 2010, 13:40
par Anonyme » 22 Juil 2010, 13:40
Bonjour tout le monde !
Un petit défi d'arithmétique :
Montrer que parmi tous les nombres de la forme

avec n un entier naturel non nul figurent tous les nombres premiers sauf 2 et 3.
Bonne chance !
P.S. : J'ai attribué à ce défi le niveau 3ème car il est normalement destiné à des élèves issus de cette classe en guise d'exercice annexe.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Juil 2010, 13:46
par Lostounet » 22 Juil 2010, 13:46
Salut,
On avait démontré que le produit de 4 entiers naturels consécutifs augmenté de 1 est un carré parfait il y a peu.
Et le produit de 4 entiers consécutifs est aussi divisible par 24...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 22 Juil 2010, 14:07
par Doraki » 22 Juil 2010, 14:07
Je vois pas tellement le rapport avec la question posée.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Juil 2010, 14:34
par Zweig » 22 Juil 2010, 14:34
Salut,
*

, donc si ce nombre est premier, alors il ne peut valoir 2 ou 3.
* il suffit de montrer que la suite

parcourt tous les entiers impairs, i.e, pour tout naturel
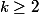
, il existe
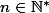
tel que :
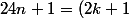^2\Leftrightarrow 6n = k(k+1))
.
)
étant toujours divisible par 6 (disjonction de cas modulo 6) pour k>1, on a le résultat voulu.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Juil 2010, 15:58
par Lostounet » 22 Juil 2010, 15:58
Moi non plus justement..! Des pistes?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Anonyme
 par Anonyme » 22 Juil 2010, 15:59
par Anonyme » 22 Juil 2010, 15:59
Moi non plus :)
Un petit indice : Déterminer lensemble E des entiers naturels n pour lesquels
V(24n + 1) est un entier.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 22 Juil 2010, 16:57
par beagle » 22 Juil 2010, 16:57
si on cherche à faire:
24n=(k-1)(k+1),
on retombe sur des k impairs et non multiples de 3, donc tous les nombres premiers sont dedans
k impair donc k-1 ou k+1 est le pair multiple de 4, on a déjà 2x4
k-1 ou k+1 multiple de 3 quand k pas multiple de 3.
2x4x3=24
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 22 Juil 2010, 18:41
par Mathx » 22 Juil 2010, 18:41
Oui, beagle, tu es sur la bonne piste. Mais il manque deux trois choses.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 22 Juil 2010, 18:42
par Zweig » 22 Juil 2010, 18:42
Il manque juste n>0 => V(24n+1) >= 5, donc 2 et 3 ne peuvent être atteints.
Mathx/Titux : T'as oublié de changé de compte ? :ptdr:
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 22 Juil 2010, 19:03
par beagle » 22 Juil 2010, 19:03
salut Titux, tu fais tellement partie des meubles que j'ai mème pas tiqué sur ton pseudo,
juste pour te dire content de te revoir dans de bonnes dispositions,
et j'ai bien aimé ton problème,
au début cela m'a intrigué,
quoi du 24 comme ça et on a les nombres premiers, cela m'épatait,
j'ai eu envie de voir.
Bonne soirée à toi.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 22 Juil 2010, 20:03
par beagle » 22 Juil 2010, 20:03
Lostounet a écrit:Salut,
On avait démontré que le produit de 4 entiers naturels consécutifs augmenté de 1 est un carré parfait il y a peu.
Et le produit de 4 entiers consécutifs est aussi divisible par 24...
finalement l'avait pas si tord le Lostounet de tilter sur tout ça,
cela ressemble,
pour faire du 24 on peut faire du 2x3x4,
et ce 2x3x4 s'obtient de façon variable selon l'exo, mais c'est bien proche.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 23 Juil 2010, 11:58
par Lostounet » 23 Juil 2010, 11:58
C'est ce que je me suis dit en postant justement, un 24, une racine truc*24 + 1..
Ce n'est pas trop trop loin!
Merci :we: :++:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
avec n un entier naturel non nul figurent tous les nombres premiers sauf 2 et 3.
