Théorie des graphes
15 messages
- Page 1 sur 1
Théorie des graphes
Bonjour,
Je recherche une formule ou un algorithme qui à partir d'un nombre de sommets k me donne le nombre d'arbres réalisables (sans compter les isomorphismes) de façon que tous les sommets soient utilisés (une seule composante connexe).
Merci d'avance,
Je recherche une formule ou un algorithme qui à partir d'un nombre de sommets k me donne le nombre d'arbres réalisables (sans compter les isomorphismes) de façon que tous les sommets soient utilisés (une seule composante connexe).
Merci d'avance,
Si je suis les valeurs de Doraki, tu considère que :
1) Les arrètes sont non orientées.
2) Que deux sommets ne peuvent pas être reliés par plus d'une arrète.
3) Il n'y a jamais d'arrète d'un sommet vers lui même.
Avant de me lancer dans les calculs, j'aurais tendance à penser qu'on peut au moins avoir une formule de récurrence dans le cas où on ne compte pas à isomorpisme de graphe prés.
Par contre, à isomorphisme prés, j'y vois pas bien beau ce truc là... (mais, mon intuition...)
1) Les arrètes sont non orientées.
2) Que deux sommets ne peuvent pas être reliés par plus d'une arrète.
3) Il n'y a jamais d'arrète d'un sommet vers lui même.
Avant de me lancer dans les calculs, j'aurais tendance à penser qu'on peut au moins avoir une formule de récurrence dans le cas où on ne compte pas à isomorpisme de graphe prés.
Par contre, à isomorphisme prés, j'y vois pas bien beau ce truc là... (mais, mon intuition...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui vous avez bien compris, je cherche la suite
f(1) = 1
f(2) = 1
f(3) = 1
f(4) = 2
etc
avec les règles
1) Les arrêtes sont non orientées.
2) Que deux sommets ne peuvent pas être reliés par plus d'une arrète. (logique)
3) Il n'y a jamais d'arrête d'un sommet vers lui même. (logique)
Pour l'isomorphisme en fait dans mon esprit ça veut dire qu'on ne cherche que les différentes structures réalisables sans prendre en compte si tel ou tel sommet est là ou ailleurs.
f(1) = 1
f(2) = 1
f(3) = 1
f(4) = 2
etc
avec les règles
1) Les arrêtes sont non orientées.
2) Que deux sommets ne peuvent pas être reliés par plus d'une arrète. (logique)
3) Il n'y a jamais d'arrête d'un sommet vers lui même. (logique)
Pour l'isomorphisme en fait dans mon esprit ça veut dire qu'on ne cherche que les différentes structures réalisables sans prendre en compte si tel ou tel sommet est là ou ailleurs.
@busard_des_roseaux : j'ai pas tout cherché à comprendre, mais il me semble que tu cherche seulement les arbres alors qu'il voudrait tout les graphes connexes (y compris les non simplement connexes...)
Perso, j'aurais procédé "par récurrence".
Partant d'un graphe connexe, si on enlève le "dernier" sommet, on obtient un graphe composé d'un certain nombre de composantes connexes (on peut écrire le nombre de possibilités) puis le "dernier sommet" doit être relié à au moins un sommet de chaque composantes pour que le résultat soit connexe.
SAUF que, c'est pas à isomorphisme prés et que, si on fait agir le groupe des permutations là dessus, il est clair que les orbites n'ont pas toutes le même nombre d'éléments donc pour calculer le nombre de classes...
L'autre truc qui me vient à l'esprit, c'est de voir le graphe comme une matrice symétrique (donc diagonalisable) avec des 0 et des 1 comme coeff.
Le "à isomorphisme prés" devient un "à changement d'ordre de la base prés" qui commence à un peu ressembler à un "à changement de base prés"... (à voir)
L'autre truc, c'est que dans ce modèle, pour repérer si le graphe est connexe, le seul truc que je vois est de mettre des 1 dans la diagonale et d'élever à la puissance au moins n : s'il n'y a plus de 0 nulle part, c'est connexe.
Est-ce repérerable à l'aide des valeurs propres de la matrice ?
Perso, j'aurais procédé "par récurrence".
Partant d'un graphe connexe, si on enlève le "dernier" sommet, on obtient un graphe composé d'un certain nombre de composantes connexes (on peut écrire le nombre de possibilités) puis le "dernier sommet" doit être relié à au moins un sommet de chaque composantes pour que le résultat soit connexe.
SAUF que, c'est pas à isomorphisme prés et que, si on fait agir le groupe des permutations là dessus, il est clair que les orbites n'ont pas toutes le même nombre d'éléments donc pour calculer le nombre de classes...
L'autre truc qui me vient à l'esprit, c'est de voir le graphe comme une matrice symétrique (donc diagonalisable) avec des 0 et des 1 comme coeff.
Le "à isomorphisme prés" devient un "à changement d'ordre de la base prés" qui commence à un peu ressembler à un "à changement de base prés"... (à voir)
L'autre truc, c'est que dans ce modèle, pour repérer si le graphe est connexe, le seul truc que je vois est de mettre des 1 dans la diagonale et d'élever à la puissance au moins n : s'il n'y a plus de 0 nulle part, c'est connexe.
Est-ce repérerable à l'aide des valeurs propres de la matrice ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, je vient d'effacer un (long) post du fait qu'une fois encore, j'avais lu de travers.... et cru qu'on cherchait les graphes connexes alors que c'est simplement les arbres... (ce qui m'a mis dedans, c'est la parenthèse parlant d'une seule composante connexe...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
salut,
voilà une id'algo :
on a n noeuds
on part de root
root possède de 1 à n-1 sous-arbres.
si 1 seul sous-arbre, on se rappèle avec n-1 noeuds
sinon
on va trier : le premier sous-arbre doit etre l'arbre qui contient le PLUS(sens large) de noeuds.
cqui evite les permutations avec les autres sous arbres de root. (on les ordonne).
de fait supposons qu'on ait n-1 noeuds à repartir pour 5 sous-arbres.
alors on fait 5 boucles imbriquées
i = n-1 ;i>4; i--
j = i ;...; j--
k = j -1;...
si i+j+k+...+n == n-1
alors on rappele la procédure pour chacun des sous arbres
etc
et chaque combinaison nous donne alors un graphe différent.
finsi
c'est un peu brut, pis alors le temps...espérons que n soit pas trop grand lol
voilà une id'algo :
on a n noeuds
on part de root
root possède de 1 à n-1 sous-arbres.
si 1 seul sous-arbre, on se rappèle avec n-1 noeuds
sinon
on va trier : le premier sous-arbre doit etre l'arbre qui contient le PLUS(sens large) de noeuds.
cqui evite les permutations avec les autres sous arbres de root. (on les ordonne).
de fait supposons qu'on ait n-1 noeuds à repartir pour 5 sous-arbres.
alors on fait 5 boucles imbriquées
i = n-1 ;i>4; i--
j = i ;...; j--
k = j -1;...
si i+j+k+...+n == n-1
alors on rappele la procédure pour chacun des sous arbres
etc
et chaque combinaison nous donne alors un graphe différent.
finsi
c'est un peu brut, pis alors le temps...espérons que n soit pas trop grand lol
la vie est une fête 
Salut,
Peut être que ça: http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Kirchhoff
pourrait t'aider
Peut être que ça: http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Kirchhoff
pourrait t'aider
re,
en plus de la difficulté du dénombrement (intrinsèque, il faut gérer
le nombre de partitions) d'un entier
d'un entier  )
)
il y a le souci de travailler à "isomorphisme près".
dans on rajoute des arêtes à l'arbre (k=1;2;3;4;5..)
on trouve des dessins d'arbres qui peuvent se correspondre par réflexion (symétrie axiale) et sont donc homéomorphes. :doh:
en plus de la difficulté du dénombrement (intrinsèque, il faut gérer
le nombre de partitions
il y a le souci de travailler à "isomorphisme près".
dans on rajoute des arêtes à l'arbre (k=1;2;3;4;5..)
on trouve des dessins d'arbres qui peuvent se correspondre par réflexion (symétrie axiale) et sont donc homéomorphes. :doh:
Sans le "à isomorphisme prés", c'est à dire en numérotant les sommets, je voterais (sans totale certitude) pour :
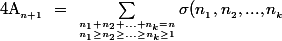\,n_{_{1}}A_{_{n_1}}\,n_{_{2}}A_{_{n_2}}...n_{_{k}}A_{_{n_k}})
où=\frac{n!}{n_1!n_2!...n_k!q_1!q_2!q_3!...) avec
avec 
De plus, pour en "rajouter" par rapport à busard_des _roseaux, un arbre peut avoir des tas d'automorphisme : l'arbre avec n-1 feuilles plus un sommet de degrés n-1 a un groupe d'automorphisme isomorphe au groupe des permutation de {1..n-1} !
où
De plus, pour en "rajouter" par rapport à busard_des _roseaux, un arbre peut avoir des tas d'automorphisme : l'arbre avec n-1 feuilles plus un sommet de degrés n-1 a un groupe d'automorphisme isomorphe au groupe des permutation de {1..n-1} !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est (aprés des calculs un peu pourris)... ce que je trouve en partant de la formule ci dessus.
Edit : en regardant le lien, la formule dans le cas présent est la "Formule de Cayley"
et certaines des preuve ressemblent à ce que j'ai fait (c'est les plus moches et elles sont moins bourinnes que la mienne...)
Ensuite, "y'a plus qu'à" (???) regarder comment agit le groupe des permutation là dessus, plus précisément je regarderait bien pour un élément donné
là dessus, plus précisément je regarderait bien pour un élément donné  combien il y a d'arbres dont le groupe d'automorphisme contient
combien il y a d'arbres dont le groupe d'automorphisme contient  ...
...
Edit : en regardant le lien, la formule dans le cas présent est la "Formule de Cayley"
et certaines des preuve ressemblent à ce que j'ai fait (c'est les plus moches et elles sont moins bourinnes que la mienne...)
Ensuite, "y'a plus qu'à" (???) regarder comment agit le groupe des permutation
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
