Bonjour,
Je cherche à savoir s'il existe une méthode pour répondre à une question du type :
Existe t-il des graphes avec les listes de degrés suivantes ?
a) (3,3,3,3)
De tête je vois bien qu'un graphe complet à 4 sommets mais pour des cas plus durs, par exemple : (4,4,4,2,2) y aurait-il une méthode ou un algo pour répondre oui/non facilement ?
Merci d'avance pour votre aide,
Théorie des graphes : cas d'école
9 messages
- Page 1 sur 1
Bonjour,
tu peux essayer de construire la matrice d'adjacence (j'imagine que tu ne peux pas dupliquer les arêtes entre les sommets et que tu cherche des graphes non orientés), tu obtient alors un système linéaire qui admet une infinité de solution, le problème et de savoir si parmis elles au moins une est formé de 0 ou 1.
tu peux essayer de construire la matrice d'adjacence (j'imagine que tu ne peux pas dupliquer les arêtes entre les sommets et que tu cherche des graphes non orientés), tu obtient alors un système linéaire qui admet une infinité de solution, le problème et de savoir si parmis elles au moins une est formé de 0 ou 1.
Oui voilà ça c'est la méthode que j'applique mais je le fais plus ou moins au hasard de tête sans appliquer une méthode précise. Ça peut être assez long quand en plus on doit chercher le nombre de graphes réalisables (à isomorphisme près).
S'il existe un algo formel qui permet de passer d'une liste de degrés à une liste d'adjacence je suis preneur.
C'est bien de graphes non orientés dont il s'agit.
S'il existe un algo formel qui permet de passer d'une liste de degrés à une liste d'adjacence je suis preneur.
C'est bien de graphes non orientés dont il s'agit.
Salut,
S'il y a sommets et que tu note
sommets et que tu note ) la liste des degrés avec
la liste des degrés avec 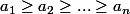 , des conditions nécéssaires (et je pense suffisantes) sont :
, des conditions nécéssaires (et je pense suffisantes) sont :
- Il faut que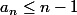 (évident)
(évident)
- La somme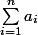 doit être paire vu que le nombre total d'arrêtes
doit être paire vu que le nombre total d'arrêtes  vérifie
vérifie 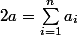
- Pour tout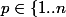 on doit avoir
on doit avoir }{2}) où
où  est le nombre d'arrêtes (en fait, il suffit de vérifier cette inégalité pour le plus grand indice
est le nombre d'arrêtes (en fait, il suffit de vérifier cette inégalité pour le plus grand indice  tel que
tel que 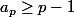 )
)
Cette dernière condition vient du fait que, si on groupe les sommets en deux :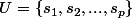 et
et 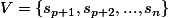 alors de chaque sommet
alors de chaque sommet 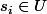 , il part au plus
, il part au plus  arrêtes allant à un autre sommet de
arrêtes allant à un autre sommet de  donc il part au moins
donc il part au moins ) arrêtes vers des sommets de
arrêtes vers des sommets de  .
.
Il y a donc au moins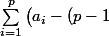\big)=\sum_{i=1}^p a_i-p(p-1)) arrêtes de
arrêtes de  vers
vers  .
.
Or, des arrêtes arrivant dans , il y en a au maximum
, il y en a au maximum 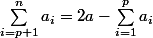
On doit donc avoir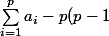\leq 2a-\sum_{i=1}^p a_i) , c'est à dire
, c'est à dire }{2}) .
.
Par exemple, pour (4,4,4,2,2), le max des tels que
tels que 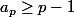 est 3 et on a
est 3 et on a }{2}) donc la configuration est impossible.
donc la configuration est impossible.
A mon avis, ces conditions sont suffisantes : je pense qu'il suffit de relier le sommet de plus grand degrés avec les sommets (autres que
de plus grand degrés avec les sommets (autres que  ) de plus grand degrés puis de recommencer avec le nouveau sommet de plus haut degrés restant...
) de plus grand degrés puis de recommencer avec le nouveau sommet de plus haut degrés restant...
S'il y a
- Il faut que
- La somme
- Pour tout
Cette dernière condition vient du fait que, si on groupe les sommets en deux :
Il y a donc au moins
Or, des arrêtes arrivant dans
On doit donc avoir
Par exemple, pour (4,4,4,2,2), le max des
A mon avis, ces conditions sont suffisantes : je pense qu'il suffit de relier le sommet
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour (4,4,2,2,2), 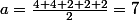 , le plus grand
, le plus grand  tel que
tel que 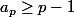 est
est 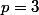 et on a
et on a }{2}) donc tout est O.K.
donc tout est O.K.
Si tu prend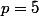 (ce n'est pas utile du fait que, si c'est O.K. pour le plus grand
(ce n'est pas utile du fait que, si c'est O.K. pour le plus grand  tel que
tel que 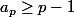 alors c'est O.K pour les autres
alors c'est O.K pour les autres  ) tu obtient :
) tu obtient : }{2})
Par contre, aprés reflexion, ces conditions ne semblent pas suffisantes...
Si tu prend
Par contre, aprés reflexion, ces conditions ne semblent pas suffisantes...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
