La notation

n'est utilisée que pour p entier, donc ça n'a pas vraiment de sens de parler de

(même si on pourrait dire que c'est juste une notation...). Dans tous les cas, la propriété

n'est ici démontrée que pour p et q entiers, et x réel positif. Avant de l'étendre aux complexes, il s'agirait de voir si elle est encore valable pour x négatif. Et c'est là qu'on tombe sur des contradictions comme le fameux
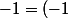^{\frac22}= \sqrt{(-1)^2}=1)
...
Dans le même ordre d'idées, on
n'a pas ^i=x^{-1})
pour tout réel x. Quand on veut définir l'élévation d'un complexe à une puissance complexe, on est obligé de violer des règles telles que
^b=x^{ab})
.
Les calculs d'Øktave et maxence6 reposent sur l'hypothèse qu'il existe une fonction puissance définie sur les complexes suffisamment sympathique pour vérifier les mêmes propriétés que la puissance réelle.
