Integrales de riemann

[enigme]

salut tout le monde!
svp j'ai un tout petit probleme a maitriser le calcul avec les integrales de riemann..
le prof n'as pas bien expliqué comment les utilisé pour montrer l'intégrabilité des integrable..
quelqu'un peut il m'expliqué un peu comment on fait s'il vous plait ??! merci d'avance

[Nightmare]

Salut,

c'est un peu vague "montrer l'intégrabilité". On a beaucoup de manière de le faire, il faut préciser à quel stade du cours. Si tu viens de voir la construction, tu as du voir une histoire de sommes inférieures et supérieures. Déjà est-ce que ça te dit quelque chose ?

[mathelot]

re,

la quadrature commence dans l'Antiquité avec Archimède
Ce grand savant parvient à mesurer l'aire d'un domaine
délimité par une parabole.

intégrale de f
A l"époque moderne, nous considérons tout d'abord les sommes de Darboux inférieures et supérieures

si f est une fonction bornée sur [a;b], on considère
une subdivision

de l'intervalle de définition



S et s sont des sommes d'aires de rectangles, majorantes et minorantes
l'aire à calculer

étant l'inf f(x) sur
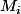étant sup f(x) sur

déf 1
f est Riemann intégrable si les deux ensembles de nombres réels:

- ensemble des aires majorantes U
- ensemble des aires minorantes V

sont des ensembles adjacents.
( U et V sont paramétrés sur toutes les subdivisions
de l'intervalle [a;b] possibles )

Dans ce cas, ils définissent une coupure au sens de Dedekind (U,V)
et un nombre réel

l=inf U= sup V

on pose

Les "coupures" sont un moyen très général de définir un nombre réel.
c'est un procédé inventé par Dedekind , basé sur la relation d'ordre, assez différent des suites de Cauchy.
Ce procédé a été repris par J Horton Conway dans les années 70.

remarque 1
typiquement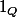 l'indicatrice des rationnels sur [a;b]
n'est pas Riemann-intégrable car les intégrales
majorantes valent b-a et les intégrales minorantes valent 0
, les ensembles U et V ne sont pas adjacents.

remarque 2
deux grandes classes de fonctions sont Riemann intégrables:
les fonctions continues car elles sont uniformément continues sur le compact [a;b]

les fonctions monotones

remarque 3
f est Riemann intégrable si et seulement si f est à variation bornée
ie, si elle est la différence entre deux fonctions croissantes

remarque 4
les fonctions croissantes peuvent être terriblement pathologiques
leurs sauts localisés sur un Cantor et sinon constantes.
regarder l'escalier du diable (brr!) ici


remarque 5
sous ces conditions de Riemann-intégrabilité, on considère
une suite numérique privilégiée, formée avec une subdivison
régulière de [a;b]


où est un point arbitraire de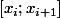
une telle somme s'appelle une somme de Riemann, elle a pour limite l'intégrale de f sur [a;b]

encore plus particulier une somme de Riemann de la forme


exemple

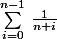a pour limite

remarque 7
en changeant un peu la mesure de longueur des bases des rectangles
de en
où g est une fonction strictement croissante, on obtient l'intégrale
de Stieltjes de f, notée évidemment



remarque 6
Lebesgue puis Denjoy viendront offrir une nouvelle version de l'intégrale plus efficace que la définition Riemannienne, en découpant non plus l'intervalle [a;b] mais l'intervalle image [m;M] et en mesurant
les images réciproques .

L'intégrale de Denjoy était tombée en désuétude , à cause de la lourdeur de sa définition mais Kurtzweil-Henstock,vers 1950, ont donné une définition toute nouvelle de l' intégrale, enfin satisfaisante, où toute fonction dérivée est intégrable (et redonne la fonction initiale f).

Ceci évite de considérer des intégrales dites "indéfinies". Cette définition moderne de l'intégrale est ou mérite d'être enseignée.

[enigme]

bon parfois on utilise l'integrabilité au voisinage de l'infini ou bien un réel, on utilise les integrales de riemann comme référence..
je ne sais comment ou quand les utilisé?

[busard_des_roseaux]

je ne sais comment ou quand les utilisé?

ni pourquoi ?

[enigme]

bon voila ma question exactement:
en classe on a écrit cette proposition : integrale de Riemann
on a :

1

bon j'ai pas compris comment utiliser ces integrales pour montrer l'integrabilité dans certain cas ? et comment savoir où les utiliser ?
voila exactement où se trouve mon probleme et merci d'avance pour votre aide..!

[busard_des_roseaux]

ici, les intégrandes ont des primitives qui s'expriment par des formes closes
(des formules ? il y a un logicien dans l'avion ? :we: )

donc, il suffit de primitiver sur un intervalle compact [1;A]
et de faire tendre A vers + l'infini.


PS: il y a une différence en logique formelle (syntaxique) entre

(formule)
et
(primitive sans formule ) ??

[JeanJ]

PS: il y a une différence en logique formelle (syntaxique) entre...
... (formule)
... (primitive sans formule ) ??

Qui a dit que la seconde intégrale n'a pas de formule ?
Tout dépend des fonctions que l'on considère comme pouvant être utilisées et celles que l'on ne veut pas utiliser pour exprimer les primitives.
- Effectivement, si on se limite aux fonctions élémentaires, la seconde intégrale "n'a pas de formule". Mais si on connait quelques fonctions d'un niveau un peu plus élevé, elle "a une formule".
- D'ailleurs la première intégrale "n'a pas de formule" pour celui qui ne connait pas encore les exponentielles.