DM trigonométrie

[hand33]

Bonjour!
Je voulais savoir ce que tu pensais des résultats que j'ai trouvé pour la troisième question:
J'ai d'abord trouvé qu'il y avait trois valeurs possibles pour x : 1, 3 et 3/2
Puis j'ai mis que de toute façon la valeur 1 était exclus par rapport à ce qu'on avait dit auparavant. Ensuite la valeur 3 est exclus car X et B seraient alors confondus et Y ne serait pas situé sur AC. Il ne reste donc que la valeur 3/2. Dans ce cas Y serait situé à 9/8 de AC. :id:

Après avoir fait ça je ne vois pas ce que veut le prof dans l'interprétation géométrique et en plus je ne voit pas comment faire pour la quatrième question. Peux-tu encore m'aider et me donner une piste?? :hein:

[Hiphigenie]

J'ai d'abord trouvé qu'il y avait trois valeurs possibles pour x : 1, 3 et 3/2
................
Ensuite la valeur 3 est exclus car X et B seraient alors confondus et Y ne serait pas situé sur AC.
...............
Dans ce cas Y serait situé à 9/8 de AC.

Il y a trois rectifications à faire ....

Réfléchis encore sur ces trois phrases :hein:

[hand33]

Ben je vois pas trop ce qu'il y a à rectifier??
Pour la première j'ai trouvé les trois valeurs à l'aide du discriminant en résolvant l'inéquation : (x²;)3)/x-1 = (9;)3)/2

Et on trouve 2 inéquations :
2(x-1) = 0
x = 1
et la deuxième :
2;)3x²-9;)3x+9;)3=0
x1 = 3
x2 = 3/2

Donc comme on avait vu avant que x ne pouvais pas prendre la valeur 1 on peut l'éliminer des solutions et ensuite si on prend la valeur 3 ce n'est pas possible car on ne respecterai pas les consignes de l'exercice. Je ne vois pas comme je pourrais expliquer ça clairement :hum:

[Hiphigenie]

Attends, on n'a pas deux équations, mais une seule...

Je te donne une rédaction de ce qu'il faut faire à partir de la question 3). Tu verras peut-être mieux l'équation en question et le reste de la résolution (interprétation graphique).

Les aires de chaque face sont égales puisque le tétraèdre est régulier. Les faces sont des triangles équilatéraux dont chaque aire est égale à .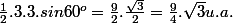

Comme il y a 4 faces dans le tétraèdre, l’aire totale tu tétraèdre est égale à .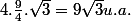


La moitié de l’aire du tétraèdre aura une aire égale à .

Si l'aire A(x) est égale à la moitié de celle du tétraèdre, alors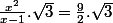 ou encore .

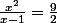Résolvons cette équation.

Condition : x – 1 0 c’est-à-dire x 1.

2x² = 9(x – 1)

2x² = 9x – 9

2x² - 9x + 9 = 0



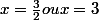
Ces valeurs de x vérifient les conditions. Elles sont donc les solutions de l’équation.

Interprétation géométrique

Si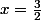 , alors le point X = I, milieu de [AB]. Le point Y sera alors égal au point C.

Dans ce cas, le triangle ASX est identique au triangle ASI c’est-à-dire à la moitié du triangle ASB, le triangle ASY est identique au triangle ASC et le triangle AXY est identique au triangle AIC c’est-à-dire à la moitié du triangle ABC.

La somme des aires .

Vu que A(ASB) = A(ASC) = A(ABC), on en déduit que = la moitié de l’aire totale du tétraèdre (qui est égale à 4.A(ASB)).


Si x = 3, alors le point X = B. Le point Y sera alors égal au point J, milieu de [AC].

Dans ce cas, le triangle ASX est identique au triangle ASB, le triangle ASY est identique au triangle ASJ c’est-à-dire à la moitié du triangle ASC et le triangle AXY est identique au triangle ABJ c’est-à-dire à la moitié du triangle ABC.

La somme des aires .

Vu que A(ASB) = A(ASC) = A(ABC), on en déduit que de l’aire totale du tétraèdre.

[hand33]

Merci beaucoup pour toutes ces précisions, je n'avais pas compris qu'il fallait faire tout cela pour l'interprétation géométrique.

Par contre, quand tu dis : Le triangle ASX est identique au triangle ASI par exemple, il ne faudrait pas plutôt parler d'égalité d'aires??

[Hiphigenie]

Non...

Ce que j'ai écrit, c'est que si x = 3/2, alors le point X est confondu avec le point I puisque AB = 3 implique que AI = 3/2.

Donc les triangles ASX et ASI sont superposés, ils sont identiques puisque X = I.

Vois-tu ?

[hand33]

D'accord!
Mais c'est que je n'étais pas sure que l'on ai le droit de dire comme ça que deux triangles étaient identiques!

[Hiphigenie]

Utilise alors le mot "superposés" ainsi il n'y aura pas d'ambiguïté.

[hand33]

Pour la dernière question, comment peut-on calculer les aires de ASX ASY et AXY si on ne sait pas où se situe le point X sur AB. Il faut utiliser le théorème de Thalès non?? :hein: :hein:

[Hiphigenie]

Oui, en sachant que le centre de gravité se trouve au tiers de la médiane à partir de la base.

[hand33]

J'arrive à trouver que AXY est un triangle équilatéral, et A(AXY)= x²;)3/4
Mais je ne vois pas comment on peut faire pour calculer l'aire de ASX et ASY ?? :hein:

[hand33]

En fait j'ai utilisé la formule de la question préliminaire et e trouve:
A(AXS) = A(ASY) = (3;)3x)/4

Par contre pour l'aire de AXY je ne suis pas sure de moi parce que je l'ai calculé avec deux formules différentes et je ne trouve pas le même résultat :
avec la première je trouve ;)3x²/4 et avec la deuxième je trouve ;)3x²/2

[Hiphigenie]

Par Thalès, je vois que tu as trouvé le rapport 2/3.

Ton calcul de A(ASX) = A(ASY) est correct mais il y a encore plus précis.

Par Thalès, tu en déduis que : AX = AY = 2

Donc

De même,

Et

D’où l’aire totale A(x) =

Or l’aire totale du tétraèdre est égale à .

Par conséquent l’aire A(x) représente les 4/9 de l’aire totale du tétraèdre. :lol3:

[hand33]

Je ne vois pas comment tu arrive à trouver 2/3 avec le théorème de thales? et aussi pour les aires de ASX et ASY je trouve le meme numerateur mais au dénominateur je trouve 4 et pas 2 ???

[Hiphigenie]

[font=Arial]Comme la droite (XY) est parallèle à [BC], les triangles AXY et ABC sont semblables.[/font]



[font=Arial]Par la réciproque de Thalès, on a : .[/font]



[font=Arial]Comme l’énoncé dit que O est le centre de gravité du triangle ABC, la droite AO coupe [BC] en son milieu que nous noterons K[/font]



[font=Arial]Le segment [AK] est alors une médiane du triangle ABC et le centre de gravité O est situé aux 2/3 de la médiane [AK] à partir de A.[/font]



[font=Arial]La relation ci-dessus peut alors se compléter par : .[/font]



[font=Arial]Or AB = AC = BC = 3.[/font]



[font=Arial]On a donc : .[/font]



[font=Arial]Par conséquent AX = 2 ; AY = 2 ; XY = 2.[/font]



[font=Arial]Le triangle AXY est équilatéral est les côtés mesurent 2 u.l.[/font]







[font=Arial]Pour les aires A(ASX) et A(ASY), si tu obtiens 4 au dénominateur, c’est parce que ton numérateur possède encore un « x » et que ce « x » peut être remplacé par 2 puisque x = AX et que AX = 2.[/font]



[font=Arial]Revois le calcul qui a été fait dans mon post de 18h29.[/font]