Racines unités
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 11:32
par barbu23 » 27 Jan 2010, 11:32
Bonjour à tous : :happy3:
J'étudie en ce moment les extensions abeliennes dont le groupe de Galois est abelien, et plus precisemment, les extensions cyclotomiques :
 $)
avec :
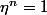
, c'est à dire,

appartient à l'ensemble des racines

- ième de l'unité ! :happy3:
Alors :
 $)
:
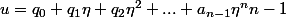
Donc :
 : \mathbb{Q}] = n $)
Est ce que vous pouvez me donner un exemple de corps intermediare entre

et
 $)
Est ce que :
 = \mathbb{Q}(1 , \eta , ... , \eta^{n-1} ) $)
( comment le pouver ?) :happy3:
Pourquoi :
 $)
est une extension maximale de

? :happy3:
Merci d'avance !

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 11:45
par barbu23 » 27 Jan 2010, 11:45
svp, je viens de voir dans un article mathematique que
:\mathbb{Q}] = \varphi (n) $)
Pouvez vous m'expliquez pourquoi ? :happy3:
Merci d'avance ! :happy3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Jan 2010, 12:02
par Doraki » 27 Jan 2010, 12:02
Parceque la famille (1, eta, eta^2 ... eta^(n-1)) n'est pas libre.
Pour n=2, c'est quoi cette famille ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 12:18
par barbu23 » 27 Jan 2010, 12:18
Doraki a écrit:Parceque la famille (1, eta, eta^2 ... eta^(n-1)) n'est pas libre.
Pour n=2, c'est quoi cette famille ?

donc pas libre ! :happy3:
Est ce que tu peux me corriger ce que je vais dire dans la suite : :happy3:
Est ce que donc :
 $)
a une structure de corps ( donc de

- d'espace vectoriel ) ? :happy3:
 : \mathbb{Q}] = n $$)
, car :
 $)
est une extension normale et séparable de

, et donc :
 : \mathbb{Q}] = n $)
avec,

est le degré galoisien, qui est egale au nombre de racines distinctes de l'unité ! :happy3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Jan 2010, 12:37
par Doraki » 27 Jan 2010, 12:37
T'es toujours en train de dire que [Q(-1) : Q] = 2 ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Jan 2010, 12:40
par Ben314 » 27 Jan 2010, 12:40
Si

est une racine
primitive (à ne pas oublier...) n-ième de l'unité, le polynôme minimal de

sur
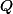
est le n-ième polynôme cyclotomique (c'est quasi. la déf. des polynômes cyclotomiques) comme le degrés de ce polynôme est
)
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 12:47
par barbu23 » 27 Jan 2010, 12:47
Doraki a écrit:T'es toujours en train de dire que [Q(-1) : Q] = 2 ?
Non,je voulais que tu me corrigse ce que j'ai écrit dans la suite, à part le fait que
 , \mathbb{Q}] = n $)
( je sais que c'est faux ) pour voir où je me suis trompé exactement ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 12:48
par barbu23 » 27 Jan 2010, 12:48
Ben314 a écrit:Si

est une racine
primitive (à ne pas oublier...) n-ième de l'unité, le polynôme minimal de

sur
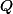
est le n-ième polynôme cyclotomique (c'est quasi. la déf. des polynômes cyclotomiques) comme le degrés de ce polynôme est
)
...
D'accord Ben314 ! Merci ! :happy3:
Et si
 n'est pas
n'est pas une racine
primitive 
- ième de u'nité, à quoi est égale :
 , \mathbb{Q}] $)
? :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 12:54
par barbu23 » 27 Jan 2010, 12:54
Est ce que :
 $)
a une structure de corps ( et donc, une structure de

- d'espace vectoriel ) ?
La famille

n'est pas libre !
Donc, quelle est exactement la structure de :
 $)
?
MErci d'avance ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Jan 2010, 13:00
par Ben314 » 27 Jan 2010, 13:00
barbu23 a écrit:Si
 n'est pas
n'est pas une racine
primitive 
- ième de u'nité
alors, c'est que c'est une racine
primitive p-ième pour un certain p qui divise n....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 27 Jan 2010, 13:03
par yos » 27 Jan 2010, 13:03
barbu23 a écrit:Est ce que :
 $)
a une structure de corps
C'est la définition de Q(truc) : plus petit sous-corps de C contenant Q et truc.
(On peut faire ça sans faire appel à un surcorps comme C mais ça revient au même.)
barbu23 a écrit:La famille

n'est pas libre !
Donc, quelle est exactement la structure de :
 $)
?
Si on dit "corps" c'est déjà pas mal comme structure non?
Pour la question initiale, îl faut en effet réviser les polynômes cyclotomiques. L'irréductibilité de ces polynômes sur Q (difficile à démontrer) entraîne
:Q]= \phi(n))
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 13:12
par barbu23 » 27 Jan 2010, 13:12
yos a écrit:C'est la définition de Q(truc) : plus petit sous-corps de C contenant Q et truc.
.
Oui, mais : dans ce cas :
 = $)
, aura une structure de

- espace vectoriel, et quelle est donc,
 = \mathrm{dim} = \phi(d) < n $)
, avec

et

est le polynome minimla de

qui est un polynome cyclotomique de degré

! c'est ça ? :happy3:
Si on dit "corps" c'est déjà pas mal comme structure non?
Pour la question initiale, îl faut en effet réviser les polynômes cyclotomiques. L'irréductibilité de ces polynômes sur Q (difficile à démontrer) entraîne
:Q]= \phi(n))
.
:Q]= \phi(d))
avec

:happy3:
Merci Yos ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 13:14
par barbu23 » 27 Jan 2010, 13:14
Ben314 a écrit:alors, c'est que c'est une racine
primitive d-ième avec

....
Oui, c'est vrai ! tu as raison ! :happy3:
Merci beaucoup à vous tous ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 13:20
par barbu23 » 27 Jan 2010, 13:20
Pour

( premier ) avec :
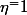
On a donc :
 , \mathbb{Q}] = p-1 $)
et
 = $)
Je voudrais que vous me citer tous les sous corps intermediaires entre

et
 $)
Merci d'avance ! :happy3:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 27 Jan 2010, 13:32
par yos » 27 Jan 2010, 13:32
barbu23 a écrit:Je voudrais que vous me citer tous les sous corps intermediaires entre

et
 $)
Et ceci quel que soit

??
Le groupe de Galois de
/Q)
est isomorphe au groupe multiplicatif (Z/nZ)*. A chaque sous groupe de (Z/nZ)* correspond un corps intermédiaire. Ca peut faire du monde.
Un célèbre théorème (Kronecker-Weber) dit que toute extension abélienne de Q est dans un certain
)
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 13:53
par barbu23 » 27 Jan 2010, 13:53
yos a écrit:Et ceci quel que soit

??
Le groupe de Galois de
/Q)
est isomorphe au groupe multiplicatif (Z/nZ)*. A chaque sous groupe de (Z/nZ)* correspond un corps intermédiaire. Ca peut faire du monde.
Un célèbre théorème (Kronecker-Weber) dit que toute extension abélienne de Q est dans un certain
)
.
Les sous groupes de
* $)
ne sont -ils pas de cette forme :
* $)
avec

? :happy3:
Ces corps intermediares entre

et
 $)
sont - ils donc de la forme
* = \mathbb{Q}(\eta=\eta_{1})/\mathbb{Q}(\eta_{2}) $)
avec :

et

? c'est ça,non ? :happy3:
avec :
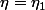
et

sont deux conjugués par rapport à leur polynome minimal ! :happy3:
Merci d'avance ! :happy3:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 27 Jan 2010, 13:59
par yos » 27 Jan 2010, 13:59
Non : Z/nZ* est pas cyclique en général.
Quant aux sous-corps de
)
, il en existe beaucoup d'autres (toujours en général). Par exemple
)
contient comme sous corps
)
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 14:13
par barbu23 » 27 Jan 2010, 14:13
Yos : :happy3:
Ah, oui, c'est vrai

est cyclique comme étant un groupe additif, par contre,
^{\times} $)
est un groupe multiplicatif qui n'est pas toujours cyclique ! :happy3:
Donc, pour que
^{\times} $)
soit cyclique, il faut mettre

( premier )
Si on est dans cette situation, est ce qu'on peut dire dans ce cas que ce que j'ai dit dans le poste avant celui là :
Les corps intermediares entre

et
 $)
sont - ils donc de la forme
* = \mathbb{Q}(\eta=\eta_{1})/\mathbb{Q}(\eta_{2}) $)
avec :

et

? c'est ça,non ? :happy3:
Merci d'avance ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 14:41
par barbu23 » 27 Jan 2010, 14:41
svp, un petit coup de main ! :happy3:
Merci d'avance ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Jan 2010, 16:41
par barbu23 » 27 Jan 2010, 16:41
svp, un petit coup de main ! :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
