Suite/Série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nico742
- Membre Naturel
- Messages: 47
- Enregistré le: 03 Oct 2007, 17:26
-
 par nico742 » 22 Nov 2009, 21:28
par nico742 » 22 Nov 2009, 21:28
Salut, j'ai un soucis sur un exo que voici :
Soit a > 0,U1 > 0, on définit la suite (Un) par : Un+1 = Un +

Dans la première question il m'était demandé de déterminer les valeurs de a pour lesquelles la suite converge, j'ai trouvé qu'il fallait avoir a > 1 à partir de la transformation suite-série.
Je bloque sur la question d'après ou il m'est demandé de donner lorsque la suite converge un équivalent de Un - l avec l sa limite.
Si quelqu'un peut me mettre sur la voie, merci d'avance !
-
bend
- Membre Relatif
- Messages: 102
- Enregistré le: 10 Nov 2009, 16:02
-
 par bend » 23 Nov 2009, 09:30
par bend » 23 Nov 2009, 09:30
Pour ta premiere quetion a>1 si juste;
Pour l'equivalent : Montre que lim l n^a * (Un- l) =1
Puis conclure que (Un -l) ~1 /(l *n^a)
 par alavacommejetepousse » 23 Nov 2009, 09:40
par alavacommejetepousse » 23 Nov 2009, 09:40
bend a écrit:Pour ta premiere quetion a>1 si juste;
Pour l'equivalent : Montre que lim l n^a * (Un- l) =1
Puis conclure que (Un -l) ~1 /(l *n^a)
bonjour
on a plutôt comme équivalent
n^{(a-1)}})
-
bend
- Membre Relatif
- Messages: 102
- Enregistré le: 10 Nov 2009, 16:02
-
 par bend » 23 Nov 2009, 10:07
par bend » 23 Nov 2009, 10:07
d'apres ton equivalence ci-dessus il faut que a >2 !!!
 par alavacommejetepousse » 23 Nov 2009, 10:25
par alavacommejetepousse » 23 Nov 2009, 10:25
bend a écrit:d'apres ton equivalence ci-dessus il faut que a >2 !!!
on parle bien de l'équivalent de u(n)-L ??
explique moi donc stp...
je te signale au passage que comme u croit elle est inférieure à sa limite et donc u(n) -L ne peut être équivalent à une suite strictement positive comme tu l'affirmes...
-
nico742
- Membre Naturel
- Messages: 47
- Enregistré le: 03 Oct 2007, 17:26
-
 par nico742 » 23 Nov 2009, 12:07
par nico742 » 23 Nov 2009, 12:07
alavacommejetepousse a écrit:bonjour
on a plutôt comme équivalent
n^{(a-1)}})
Merci
Comment le trouve-t-on?
 par alavacommejetepousse » 23 Nov 2009, 12:17
par alavacommejetepousse » 23 Nov 2009, 12:17
u(n+1) -u(n) est équivalent à 1/(l n^a)
les séries étant à termes positifs les restes sont équivalents
à gauche on a L- u(n) et à droite le reste de la série de riemann dont on trouve un équivalent en comparant avec une intégrale
-
nico742
- Membre Naturel
- Messages: 47
- Enregistré le: 03 Oct 2007, 17:26
-
 par nico742 » 23 Nov 2009, 12:56
par nico742 » 23 Nov 2009, 12:56
Ok merci je vois.
Une idée pour un équivalent de Un lorsque la suite ne converge pas?
 par alavacommejetepousse » 23 Nov 2009, 20:54
par alavacommejetepousse » 23 Nov 2009, 20:54
dans le cas où <a<1 je trouve sauf erreur u équivalente à
n^{1-a} })

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2009, 21:29
par Ben314 » 23 Nov 2009, 21:29
Lorsque les séries sont divergentes, ne connait tu pas un résultat semblable à celui que alavacommejetepousse t'a donné ?
alavacommejetepousse a écrit:u(n+1) -u(n) est équivalent à 1/(l n^a)
les séries étant à termes positifs les restes sont équivalents
à gauche on a L- u(n) et à droite le reste de la série de riemann dont on trouve un équivalent en comparant avec une intégrale
Evidement, dans ce cas, ce ne sont surement pas les reste (qui n'existent pas) qui sont équivalents.
RAJOUT SUITE AU COMENTAIRE DE DORAKI CI DESSOUS : Le théorème que j'évoque ici n'est pas directement utilisable dans l'exercice car dans le cas divergent... il n'y a plus de "l" (limite) !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par alavacommejetepousse » 23 Nov 2009, 21:33
par alavacommejetepousse » 23 Nov 2009, 21:33
Ben314 a écrit:Lorsque les séries sont divergentes, ne connait tu pas un résultat semblable à celui que alavacommejetepousse t'a donné ?
Evidement, dans ce cas, ce ne sont surement pas les reste (qui n'existent pas) qui sont équivalents.
bonsoir oui mais c'est moins simple ici car on ne peut remplacer u(n) à droite par son équivalent constant d'où un bidouillage d'intégrales

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2009, 21:57
par Ben314 » 23 Nov 2009, 21:57
Mea Culpa.....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nico742
- Membre Naturel
- Messages: 47
- Enregistré le: 03 Oct 2007, 17:26
-
 par nico742 » 23 Nov 2009, 22:01
par nico742 » 23 Nov 2009, 22:01
On m'a suggéré de montrer que :
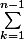
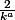
est équivalent à
}}{1-a})
Je n'arrive pas à le montrer très rigoureusement, help!
Avec ce résultat j'arriverais enfin à bout de cet exo.
merci en tout cas!
 par alavacommejetepousse » 23 Nov 2009, 22:07
par alavacommejetepousse » 23 Nov 2009, 22:07
nico742 a écrit:On m'a suggéré de montrer que :
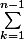
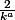
est équivalent à
}}{1-a})
Je n'arrive pas à le montrer très rigoureusement, help!
Avec ce résultat j'arriverais enfin à bout de cet exo.
merci en tout cas!
ça c'est facile c'est comme pour le cas de convergence on compare avec des intégrales mais la fin de ton exo est plus subtile (encore des intégrales)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2009, 22:19
par Ben314 » 23 Nov 2009, 22:19
J'en profite que tu est connecté alavacommejetepousse (qui visiblement a plus de bouteille que moi)
Quand on écrit une connerie (comme je l'ai fait un peu plus haut), la déontologie, c'est :
1) De l'enlever pour pas faire gourrer les lecteurs
2) De la laisser pour bien montrer qu'on est un gros nul
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par alavacommejetepousse » 24 Nov 2009, 06:01
par alavacommejetepousse » 24 Nov 2009, 06:01
Ben314 a écrit:J'en profite que tu est connecté alavacommejetepousse (qui visiblement a plus de bouteille que moi)
Quand on écrit une connerie (comme je l'ai fait un peu plus haut), la déontologie, c'est :
1) De l'enlever pour pas faire gourrer les lecteurs
2) De la laisser pour bien montrer qu'on est un gros nul
?
bonjour
ça c'est les deux options quand on est de bonne foi mais il en existe une troisième souvent utilisée qui consiste à noyer le poisson , à utiliser l'axiome du choix ou tout autre argument massue pour ne pas en démordre :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
