Résoudre un problème

par **ange1234** » 24 Aoû 2009, 10:09

Un père a 35 ans, ses enfants sont agés de 12 et 8 ans. Dans combien d'années l'âge du père égalera-t-il la somme des âges de ses enfants?

L'étude de la galaxie M87 située à 150 millions d'années lumières de la Terre révèle la présence d'un trou noir dont le diamètre serait d'environ 60 années lumières et dont la masse serait deux milliards de fois celle du soleil.
1) Sachant qu'une années lumières vaut environ 1O^13 km, calculer, en km, la distance de la Terre à cette galaxie ainsi que le diamètre du trou noir.
2) Sachant que le soleil a une masse de 2.10^30 kg, calculer en kg, la masse du trou noir.

Merci d'avance

Message hors charte : Attention, suppression du message

par **damery** » 24 Aoû 2009, 10:21

Bonjour à toi aussi!

ange1234 a écrit:Un père a 35 ans, ses enfants sont agés de 12 et 8 ans. Dans combien d'années l'âge du père égalera-t-il la somme des âges de ses enfants?.

Qu'est-ce que tu as commencé à faire....?tu veux comprendre ou juste la réponse...?

L'étude de la galaxie M87 située à 150 millions d'années lumières de la Terre révèle la présence d'un trou noir dont le diamètre serait d'environ 60 années lumières et dont la masse serait deux milliards de fois celle du soleil
1) Sachant qu'une années lumières vaut environ 1O^13 km, calculer, en km, la distance de la Terre à cette galaxie ainsi que le diamètre du trou noir.
2) Sachant que le soleil a une masse de 2.10^30 kg, calculer en kg, la masse du trou noir.

Idem, as-tu déja fais quelque chose? qu'est-ce qui te bloque?
Cordialement,

par **Paradox** » 24 Aoû 2009, 11:59

La méthode pour trouver la réponse, c'est de traduire l'énoncé sous forme mathématique. Chaque variable correspond à une donnée du problème, et les variables sont liées entre elles par une équation :)
Ici par exemple,
p = 35 (âge du père)
x = 12 (enfant 1)
y = 8 (enfant 2)
a = ? (inconnue, nombre d'années)

On veut savoir combien d'années a il faut ajouter à ces 3 personnes pour que l'âge du père = la somme des âges de ses gosses.

Y'a plus qu'à mettre tout ça en équation :)

par **yvelines78** » 24 Aoû 2009, 12:21

bonjour,

L'étude de la galaxie M87 située à 150 millions d'années lumières de la Terre révèle la présence d'un trou noir dont le diamètre serait d'environ 60 années lumières et dont la masse serait deux milliards de fois celle du soleil.
1) Sachant qu'une années lumières vaut environ 1O^13 km, calculer, en km, la distance de la Terre à cette galaxie ainsi que le diamètre du trou noir.
c'est un cas de proportionnalité
si 1 AL<---->10^13 km
150 000 000 =15*10^? AL--->........km
60 000 000=6*10^? AL---->....km

2) Sachant que le soleil a une masse de 2.10^30 kg, calculer en kg, la masse du trou noir.
la masse du trou noir=2 milliards*la masse du soleil=.........kg

après ce sont des calculs de puissance avec les formules :
a^n*a^m=a^(n+m)

a^n/a^m=a^(n-m)

par **oscar** » 24 Aoû 2009, 12:50

Bonjour

Soit x le nombre d' années
A ce moment : âge du père; des fils=

Equation:

par **ange1234** » 24 Aoû 2009, 14:32

damery a écrit:Bonjour à toi aussi!

Qu'est-ce que tu as commencé à faire....?tu veux comprendre ou juste la réponse...?

Idem, as-tu déja fais quelque chose? qu'est-ce qui te bloque?
Cordialement,

Un grand merci d'avoir répondu,
Mon problème c'est que je n'arrive pas à mettre mon énoncé en équation mathématique :triste:

par **mathelot** » 24 Aoû 2009, 16:48

bonjour,

les nombres inconnus sont nommés par des lettres x,y,z,t...

ensuite, dans la phase de modélisation, on traduit
l'énoncé du problème en égalités.

Les égalités comportant des lettres s'appellent des équations.

Dans la phase de résolution du problème,

On résoud ces équations, c'est à dire que l'on trouve la
ou les valeurs qui conviennent pour le nombre

inconnu.

exemple: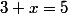

La valeur 2 convient pour

.

on résoud l'équation en retranchant 3 aux deux expressions

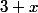et

qui sont égales
et restent égales après soustraction. :doh:

par **Sve@r** » 25 Aoû 2009, 13:48

ange1234 a écrit:
ange1234 a écrit:Un père a 35 ans, ses enfants sont agés de 12 et 8 ans. Dans combien d'années l'âge du père égalera-t-il la somme des âges de ses enfants?

Mon problème c'est que je n'arrive pas à mettre mon énoncé en équation mathématique :triste:

Aujourd'hui, on est au temps 0. A ce temps 0, l'age du père est 35 est l'age des enfants 12 et 8.
L'année prochaine, l'age du père sera 35 + 1 et ceux des enfants 12 + 1 et 8 + 1.
Dans 2 ans, l'age du père sera 35 + 2 et ceux des enfants 12 + 2 et 8 + 2.

Dans "x" ans, quel sera l'âge du père ? Et l'âge des 2 enfants ?
L'équation c'est juste rajouter une égalité entre les 2 expressions répondant à ces 2 questions.

par **ange1234** » 25 Aoû 2009, 18:25

Sve@r a écrit:Aujourd'hui, on est au temps 0. A ce temps 0, l'age du père est 35 est l'age des enfants 12 et 8.
L'année prochaine, l'age du père sera 35 + 1 et ceux des enfants 12 + 1 et 8 + 1.
Dans 2 ans, l'age du père sera 35 + 2 et ceux des enfants 12 + 2 et 8 + 2.

Dans "x" ans, quel sera l'âge du père ? Et l'âge des 2 enfants ?
L'équation c'est juste rajouter une égalité entre les 2 expressions répondant à ces 2 questions.

Un grand merci, grâce à vous j'y suis arrivée ..

par **Sve@r** » 26 Aoû 2009, 06:06

ange1234 a écrit:Un grand merci, grâce à vous j'y suis arrivée ..

Tu devrais nous montrer le résultat. Déjà on pourra te dire si c'est ok, et même te donner des conseils pour y arriver plus vite...

Résoudre un problème

Résoudre un problème

Merci

Qui est en ligne