Oui
mais le soucis est qu'ici on x n'est pas réel.
1=2
52 messages
- Page 3 sur 3 - 1, 2, 3
Bonjour, on sent bien que c'est la deuxième égalité qui va pas, reste à trouver la raison de fond. Je n'y connais pas grand-chose en analyse complexe mais ce qui me semble clair c'est que, de la même façon que ^1 \neq ((-1)^2)^{\frac12}) , on n'a pas
, on n'a pas 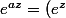^a) .
.
J'imagine que c'est dû au fait que pour calculer^a) , on doit recourir à une détermination du log complexe, et poser
, on doit recourir à une détermination du log complexe, et poser ^a = e^{a Ln(e^z)}) . Sauf que la valeur de
. Sauf que la valeur de ) doit changer selon la détermination du log qu'on choisit...
doit changer selon la détermination du log qu'on choisit...
J'imagine que c'est dû au fait que pour calculer
uztop a écrit:Le problème dans le message de Mathusalem est bien
En fait, cachender a raison en disant quen'existe pas; la racine carrée n'est définie que pour des réels positifs.
Dans le corps des complexes, on définittel que
mais on ne peut pas écrire
. Cette notation est abusive et dangereuse puisqu'elle permettrait des raisonnements faux comme celui présenté par Mathusalem.
Tout à fait d'accord et c'est bien la seule explication.
Dominique Lefebvre a écrit:Bonsoir,
1^n = 1 : cela n'est-il pas vrai que si n est un entier positif, ce qui n'est manifestement pas le cas ici...
Je ne suis pas tout à fait d'accord, comme 1 est strictement positif alors
oui Skullkid tu tiens l'explication.
D'ailleurs si on veut faire simple, si on prend le ln de on trouve
on trouve  ce qui montre bien qu'il faut faire gaffe avec les log de nombre complexe.
ce qui montre bien qu'il faut faire gaffe avec les log de nombre complexe.
Mais alors c'est quoi la règle ?
Si alors
alors ou
ou 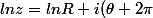) mais comment choisir ? quelle est la règle ? Ca n'est pas très clair pour moi ?
mais comment choisir ? quelle est la règle ? Ca n'est pas très clair pour moi ?
D'ailleurs si on veut faire simple, si on prend le ln de
Mais alors c'est quoi la règle ?
Si
Personnellement, lorsque j'ai découvert ce pseudo-paradoxe, je m'y connaissait très peu en analyse complexe et celui-ci m'a permis de beaucoup apprendre rien qu'en cherchant sa solution.
C'est effectivement une histoire de détermination du logarithme, et même avec ça, on n'aura pas dans le cas général log(ab) = log a + log b. Il suffit de prendre l'exemple d'Ericovitchi pour s'en convaincre. Ainsi la formule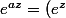^a) pour tout a réel est fausse. Pour a entier ça marche vu que l'on n'utilise pas la notion de logarithme.
pour tout a réel est fausse. Pour a entier ça marche vu que l'on n'utilise pas la notion de logarithme.
C'est effectivement une histoire de détermination du logarithme, et même avec ça, on n'aura pas dans le cas général log(ab) = log a + log b. Il suffit de prendre l'exemple d'Ericovitchi pour s'en convaincre. Ainsi la formule
52 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
