1=2
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Kah
- Membre Rationnel
- Messages: 540
- Enregistré le: 15 Sep 2008, 19:51
-
 par Kah » 10 Déc 2008, 20:00
par Kah » 10 Déc 2008, 20:00
Euler911 a écrit:Une autre:
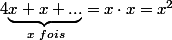
Si on dérive membre à membre:
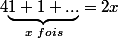
Donc x=2x
D'où 1=2
CQFD :ptdr:
:doh: :doh:
Heu quelqu'un aurait une explication? je sens que sinon, je ne vais pas dormir ce soir.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Déc 2008, 20:17
par Doraki » 10 Déc 2008, 20:17
T'arrives à voir ce que ça veut dire "x + x + ... + x (x fois)" pour x = genre euh.. pi, toi ?
-
Sve@r
 par Sve@r » 10 Déc 2008, 20:17
par Sve@r » 10 Déc 2008, 20:17
Euler911 a écrit:Une autre:
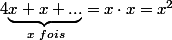
Si on dérive membre à membre:
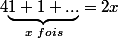
Donc x=2x
D'où 1=2
CQFD :ptdr:
Pas mal. Mais je pense que la loi "dérivée d'une somme = somme des dérivées" ne s'applique que si on dérive une somme quantifiée (constante) de fonctions.
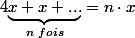
Si on dérive membre à membre:
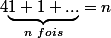
Toi, t'appliques cette loi sur une somme de fonctions dépendant du paramètre x. Je ne sais pas comment le dire avec des mots mathématiques mais en tout cas c'est interdit...
Kah a écrit::doh: :doh:
Heu quelqu'un aurait une explication? je sens que sinon, je ne vais pas dormir ce soir.
Pour moi, mon seul credo est la citation de M. Spock dans le film
Star Trek VI - Terre inconnue qui dit
M. Spock a écrit:Même la logique doit s'effacer devant la physique
Si une démo prouve un truc incohérent, c'est que la démo se quiche quelque part. :id:
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 10 Déc 2008, 20:18
par Euler911 » 10 Déc 2008, 20:18
Oui je sais:P J'abuse de la définition de la multiplication...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 10 Déc 2008, 20:23
par leon1789 » 10 Déc 2008, 20:23
Euler911 a écrit:Une autre:
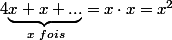
Si on dérive membre à membre:
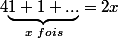
Donc x=2x
D'où 1=2
CQFD :ptdr:
oui, amusante celle là !
Quand j'étais en terminale, on me l'avait fait aussi :zen:
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 10 Déc 2008, 20:23
par Euler911 » 10 Déc 2008, 20:23
Sve@r a écrit:Si une démo prouve un truc incohérent, c'est que la démo se quiche quelque part.
On-ne-peut-plus-logique.
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 12 Juin 2009, 19:55
par Bastien L. » 12 Juin 2009, 19:55
Bonsoir,
Je ne sais si j'ai raison, mais il m'a semblé que les arguments donnés quelques pages avant pour infirmer la "démonstration" que 1+1=0 ne sont pas suffisants
Est-ce que je me trompe?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 12 Juin 2009, 20:13
par Euler911 » 12 Juin 2009, 20:13
Mais encore?
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 12 Juin 2009, 20:29
par Bastien L. » 12 Juin 2009, 20:29
Je ne vois pas pourquoi le message n°11, où Sve@r explique qu'on a considéré
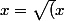)
infirme la relation, puisque, je crois, c'est bien pour le nombre 1 qu'on a fait ça...
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 12 Juin 2009, 21:12
par uztop » 12 Juin 2009, 21:12
Le problème dans le message de Mathusalem est bien
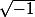
En fait, cachender a raison en disant que
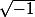
n'existe pas; la racine carrée n'est définie que pour des réels positifs.
Dans le corps des complexes, on définit

tel que
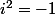
mais on ne peut pas écrire
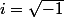
. Cette notation est abusive et dangereuse puisqu'elle permettrait des raisonnements faux comme celui présenté par Mathusalem.
-
Bastien L.
- Membre Relatif
- Messages: 308
- Enregistré le: 12 Oct 2008, 02:33
-
 par Bastien L. » 12 Juin 2009, 21:20
par Bastien L. » 12 Juin 2009, 21:20
D'accord. Passionnant, tout ça! Et très important... :-) Merci!
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 22 Juin 2009, 16:49
par oscar » 22 Juin 2009, 16:49
Bonjour
Encore un paradoxe?? Deux nombres différents sont égaux !!
Soit les nombres a et b tels que a # b; c leur moyenne arithmétique.
a + b = 2c
=> ( a+b) (a-b) = 2c (a-b) ou a² - b² = 2ac -2bc.
On peut écrire a²-2ac = b² - 2bc et a² - 2ac +c² = b² - 2bc+ c²
ou ( a - c)² = ( b - c)²
En extrayant la racine carrée des deux membres , on obtient a - c = b - c
ou a = b
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Juin 2009, 17:08
par Joker62 » 22 Juin 2009, 17:08
On extrait pas les racines pareil en Belgique :p ?
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Juin 2009, 03:51
par quinto » 23 Juin 2009, 03:51
uztop a écrit:Dans le corps des complexes, on définit

tel que
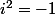
mais on ne peut pas écrire
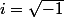
. Cette notation est abusive et dangereuse puisqu'elle permettrait des raisonnements faux comme celui présenté par Mathusalem.
Ce n'est pas le problème, c'est juste une notation ...
Le problème est caché dans la propriété de morphisme.
-
Anonyme
 par Anonyme » 23 Juin 2009, 12:23
par Anonyme » 23 Juin 2009, 12:23
oscar a écrit:Bonjour
Encore un paradoxe?? Deux nombres différents sont égaux !!
Soit les nombres a et b tels que a # b; c leur moyenne arithmétique.
a + b = 2c
=> ( a+b) (a-b) = 2c (a-b) ou a² - b² = 2ac -2bc.
On peut écrire a²-2ac = b² - 2bc et a² - 2ac +c² = b² - 2bc+ c²
ou ( a - c)² = ( b - c)²
En extrayant la racine carrée des deux membres , on obtient a - c = b - c
ou a = b
On ne peut pas extraire la racine carre de cette facon
Premièrement il faut considéré que a >b donc a>c et b<c
En extrayant la racine carre de ( a - c)² on obtient a-c
mais en extrayant la racine carre de ( b - c)² on obtient c-b et non b-c
a la fin on obtient a-c=c-b ce qui est correct
-
Pafapafadidel
- Membre Naturel
- Messages: 87
- Enregistré le: 30 Mar 2009, 16:38
-
 par Pafapafadidel » 21 Aoû 2009, 12:25
par Pafapafadidel » 21 Aoû 2009, 12:25
J'en ai une, j'en ai une, j'en ai une!
Pour tout
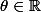
,
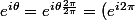^{\frac{\theta}{2\pi}}=1^{\frac{\theta}{2\pi}}=1)

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 21 Aoû 2009, 13:48
par Ericovitchi » 21 Aoû 2009, 13:48
Oui il est vraiment bien celui-là Pafa !! :pc: Et puis comme ça, je ne vois pas le biais ? qui a une idée ?
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 21 Aoû 2009, 13:54
par Jack the ripper » 21 Aoû 2009, 13:54
C'est un peu trop facile de dire ça mais je crois que le problème vient de la puissance, j'avais déjà vu quelque chose du type quelque part il me semble ...
 par Dominique Lefebvre » 21 Aoû 2009, 14:21
par Dominique Lefebvre » 21 Aoû 2009, 14:21
Ericovitchi a écrit:Oui il est vraiment bien celui-là Pafa !! :pc: Et puis comme ça, je ne vois pas le biais ? qui a une idée ?
Bonsoir,
1^n = 1 : cela n'est-il pas vrai que si n est un entier positif, ce qui n'est manifestement pas le cas ici...
-
Benjamin
- Membre Complexe
- Messages: 2337
- Enregistré le: 14 Avr 2008, 10:00
-
 par Benjamin » 21 Aoû 2009, 14:31
par Benjamin » 21 Aoû 2009, 14:31
Bonjour,
Etant donné que x^alpha = exp(alpha*ln(x)), si x=1, on a bien 1^alpha=1 pour tout alpha...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
tel que
mais on ne peut pas écrire
. Cette notation est abusive et dangereuse puisqu'elle permettrait des raisonnements faux comme celui présenté par Mathusalem.