Dérivée du cos et du sin (démo)

[egan]

Salut,
Je me demandais comment on pouvait démontrer les résultats portant sur les dérivées respectives des fonctions sinx et cosx.
J'ai cherché à la faire avec la définition, mais je n'ai rien trouvé de glorieu.
Ensuite je suis partie sur cette idée:



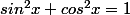
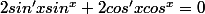
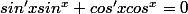
Il faudrait pouvoir montrer que les solutions sont forcément sin'x=kcosx et cos'x=-ksinx.
Mais même en admettant cela (à supposer que se soit juste), la détermination du k n'est pas simple.
Vous en pensez quoi ?
@+ Boris.

[Skullkid]

Il me semble que c'est pas possible sans passer par la définition en série entière ou (ce qui revient un peu au même) l'exponentielle complexe.

[oscar]

voici la demo


http://img199.imageshack.us/i/deriveecosxetsins.jpg/

[girdav]

Tout dépend comment ils montrent le résultat sur les limites.

[egan]

Oui j'allais dire la même chose. La démo de ces limites se fait aussi en connaissant les résultats que l'on veut montrer.

[Skullkid]

La limite de sinx / x en 0 peut se calculer géométriquement, mais je ne connais pas de démo pour celle de (cosx - 1) / x ... Mais ça ne veut pas dire qu'il n'y en a pas ! Pourrait-on avoir un scan des pages 73 et 68 ? ^^