Suite croissante
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lucie68
- Membre Naturel
- Messages: 60
- Enregistré le: 21 Fév 2009, 17:44
-
 par lucie68 » 16 Juin 2009, 09:03
par lucie68 » 16 Juin 2009, 09:03
Bonjour :)
Je me demandais comment montrer que la suite (un) définie par récurrence par :
un+1 = racine ( un + 1 )
uo=1
est croissante.
J'ai une idée mais j'aurais juste aimé que vous me corrigiez si c'est faux.
Comme l'application f associée est croissante, on a que (un) est monotone.
La croissante de (un) dépend donc du signe de u1-u0.
Or u1-u0 = racine(2) -1 donc u1 -u0 est positive et on peut montrer par récurrence que (un) est croissante.
Merci :)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Juin 2009, 09:06
par Clembou » 16 Juin 2009, 09:06
lucie68 a écrit:Bonjour

Je me demandais comment montrer que la suite (un) définie par récurrence par :
un+1 = racine ( un + 1 )
uo=1
est croissante.
J'ai une idée mais j'aurais juste aimé que vous me corrigiez si c'est faux.
Comme l'application f associée est croissante, on a que (un) est monotone.
La croissante de (un) dépend donc du signe de u1-u0.
Or u1-u0 = racine(2) -1 donc u1 -u0 est positive et on peut montrer par récurrence que (un) est croissante.
Merci

Bonjour,
Tu ne peux pas faire la méthode classique qui montre que
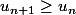
? :hein:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 16 Juin 2009, 09:16
par ffpower » 16 Juin 2009, 09:16
Je ne sais pas si on peut prouver directement sans reccurence,mais sa demo est juste en tout cas..
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Juin 2009, 09:18
par Clembou » 16 Juin 2009, 09:18
ffpower a écrit:Je ne sais pas si on peut prouver directement sans reccurence,mais sa demo est juste en tout cas..
Oui, je n'ai pas dit le contraire :++: Je voulais juste savoir si on pouvait passer par la méthode classique.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Juin 2009, 11:23
par Nightmare » 16 Juin 2009, 11:23
Clembou a écrit:Oui, je n'ai pas dit le contraire :++: Je voulais juste savoir si on pouvait passer par la méthode classique.
Qu'appelles-tu méthode classique? La méthode employée ici est simple et classique des études de suite.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Juin 2009, 11:46
par Clembou » 16 Juin 2009, 11:46
Je voulais directement voir que
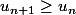
. Mais il est vrai que la démonstration est correcte :++:
-
lucie68
- Membre Naturel
- Messages: 60
- Enregistré le: 21 Fév 2009, 17:44
-
 par lucie68 » 16 Juin 2009, 15:08
par lucie68 » 16 Juin 2009, 15:08
J'avais essayé la méthode 'classique ' mais je ne voyais pas trop comment faire, c'est pour ça que j'ai fait comme ça !
Merci en tout cas!
-
kolmogorov
- Membre Naturel
- Messages: 10
- Enregistré le: 14 Juin 2009, 11:06
-
 par kolmogorov » 16 Juin 2009, 17:24
par kolmogorov » 16 Juin 2009, 17:24
salut
essayer de montrer que
U(n+1)/U(n) est plus grand que 1
donc la suite est croissante
bonne chance
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 17 Juin 2009, 06:09
par ft73 » 17 Juin 2009, 06:09
La première méthode citée me semble la meilleure.
Si on fait

du même signe que

qui fait apparaître

(-x^2+x+1, je ne sais pas pq le forum me met ce "p" !!!!!)
dont la racine positive est

, ce qui obligerait à montrer que la suite est majorée par le nombre d'or

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
