Suite croissante de fonctions harmoniques

[Nightmare]

Bonsoir à tous :happy3:

En étudiant les fonctions harmoniques, j'ai conjecturé un résultat, je ne sais pas s'il est vrai, et si c'est le cas s'il est supposé connu. En tout cas s'il est vrai, je n'arrive pas à le démontrer !

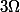
On se donne une suite croissante de fonctions harmoniques (ie de Laplacien nul) sur un domaine à priori quelconque alors :

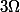
Soit sur tout entier.

Soit converge localement uniformément (ie sur tout compact) et sa limite est harmonique.

Ce qui m'a fait conjecturer le résultat est que sur un disque quelconque, une fonction harmonique coïncide avec son intégrale de poisson. Ainsi, au vue des inégalités que l'on a sur le noyau de Poisson, il semble que l'on puisse borner sur tout compact les variations de notre suite de fonction harmonique. Cependant, je n'arrive pas à rédiger...

Si vous aviez une piste !

Merci
:happy3:

[Lemniscate]

Salut,

Ta suite est croissante. Cela veut-il dire que , est croissante ?

Si ta suite est croissante donc, cela veut dire que tu es sur ?

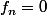
A ce moment la Laplacien de est équivalent à sur non ?
Donc on peut remplacer les d ronds par des d droits ?

Je préfère pas me lancer dans une démo si j'ai pas compris les hypothèses...

[Nightmare]

Oui bien sûr les fonctions sont à valeurs dans R.

Pour la suite on est d'accord, mais pour le moment ça ne nous avance à rien !

[Lemniscate]

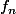
Je peux me tromper mais la condition du laplacien nul ne te donne-t-il pas que chaque est affine ?

Après reste à utiliser la croissance de ta suite de fonctions en tout z de et là je bloque !

[Nightmare]

Euh non ! On est dans R² (ou C), plus dans R.

Le laplacien nul se traduit par ce qui n'implique surement pas que f est affine !

[R.C.]

Bonjour,
Est-ce qu'il ne manquerait ma une ou deux hypothèses : si je prend fn = n (fonction constante) c'est pas près de converger.
Sinon, sur une note plus optimiste, il me semble que tu as un resultat de compacité du même style avec des fonctions holomorphes, donc vu leur relations intimes, ca peut peut etre le faire...

[Nightmare]

R.C :

Oui, en relisant mon énoncé, j'ai vu une erreur, je voulais écrire :

[Nightmare]

En fait il suffit de montrer que si ça ne diverge vers oo alors ça converge et que la limite est harmonique. Le théorème de Dini nous donnera la convergence uniforme locale.