Exercice sur la méthode de Newton, l'algorithme de Babylone

[argent2000]

Bonjour tout le monde, J'ai du mal avec cet exercice, pourriez-vous m'aider?
Je remercie d'avance tous ceux qui prendront le temps de me répondre!!



Soit la courbe C d'équation : y=x^3-5 , cette courbe coupe l'axe des abscisses au point d'abscisse ³;)5. On cherche à trouver une valeur approchée de ce nombre.

1. Tracer la courbe C ( unité 2 cm), placer A0 d'abscisse x0 = 1 sur cette courbe et tracer la tangente en A0 à la courbe C

2. Donner l'équation de la tangente et l'abscisse x1 du point d'intersection de cette tangente avec l'axe Ox.

3. Plus généralement on note xn > 0 l'abscisse d'un point An de la courbe C et x n+1 l'abscisse du point d'intersection de la tangente en An à la courbe C avec l'axe des abscisses. On poursuit les constructions selon le même algorithme et on construit ainsi une suite (xn). Justifier que:

x n+1 = 1/3(2x n + (5/x^2 n))

4. Compléter le tableau suivant:

n Xn x³n
0 1 1
1 2, 333 333 333 12, 703 703 703
… … …

5. Remarque ? Essayer en remplaçant 5 par 29 par exemple et comparer avec la valeur fournie par la calculatrice pour ³;)29.

[uztop]

Rebonjour,
tu veux faire les deux exercices en même temps ? Il vaudrait mieux en choisir un pour commencer.

[mathelot]

aloha,

Une difficulté de l'exercice est le nombre de variables à utiliser. Je conseille les notations suivantes,compatibles avec l'énoncé:

(x,f(x)) coordonnées du point M (générique) de la courbe de f.

(X,Y) coordonnées d'un point N du plan pour écrire une équation
de la tangente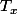 en M

écrire l'équation de la droite tangente (x fixé)

si et seulement si

ensuite, on définit la suite de terme général de la méthode de Newton.