Fraction rationnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rostand
- Messages: 4
- Enregistré le: 31 Jan 2009, 20:57
-
 par rostand » 31 Jan 2009, 21:05
par rostand » 31 Jan 2009, 21:05
bonsoir
voici un exercice ou l'on me demande de Decomposer la fraction rationnelle
1/X^2(X-1)^n
(on pourra poser Y=X-1 )
j'applique la formule mais après je peux plus rien faire.Et je ne crois pas qu'on me demande juste la structure de la decomposition :help:

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 31 Jan 2009, 21:16
par leon1789 » 31 Jan 2009, 21:16
1/Y^n(Y+1)^2
A priori, quelle est la forme de la décomposition en éléments simples ?
-
rostand
- Messages: 4
- Enregistré le: 31 Jan 2009, 20:57
-
 par rostand » 01 Fév 2009, 00:13
par rostand » 01 Fév 2009, 00:13
:help: :mur:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Fév 2009, 01:11
par barbu23 » 01 Fév 2009, 01:11
Bonsoir :
Si ma mémoire est bonne, voiçi comment on procède :
Il s'agit de determiner les scalaires :

et

tels que :
^{n}} = \frac{a_{1}}{X}+ \frac{a_{2}}{X^{2}} + \displaystyle \sum_{k=1}^{n} \frac{b_{k}}{(X-1)^{k} $)
Cette écriture s'appelle décomposition en fractions rationnelles.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Fév 2009, 01:21
par barbu23 » 01 Fév 2009, 01:21
Par exemple, pour détérminer :
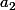
, on multiplie les deux membres de l'égalité par :

, ensuite, on met :
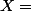
par exemple : et on obtient :
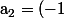^{n} $)
, c'est tellement simple ! il suffit de comprendre le principe et ça ira pour tout le reste ! c'est pas grand chose !
Cordialement !
-
Lemniscate
- Membre Relatif
- Messages: 300
- Enregistré le: 18 Jan 2009, 19:55
-
 par Lemniscate » 01 Fév 2009, 01:40
par Lemniscate » 01 Fév 2009, 01:40
barbu23 a écrit:Par exemple, pour détérminer :
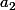
, on multiplie les deux membres de l'égalité par :

, ensuite, on met :
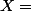
par exemple : et on obtient :
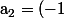^{n} $)
, c'est tellement simple ! il suffit de comprendre le principe et ça ira pour tout le reste ! c'est pas grand chose !
Cordialement !
Sauf que là comme n peut être grand, c'est pas aussi évident qu'une fraction où les puissances ne dépassent pas 3 ! Par exemple, pour trouver tous les
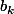
ce n'est pas évident ...
-
rostand
- Messages: 4
- Enregistré le: 31 Jan 2009, 20:57
-
 par rostand » 01 Fév 2009, 16:12
par rostand » 01 Fév 2009, 16:12
a1 et les bk ne sont pas si simlples :triste:
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 01 Fév 2009, 16:27
par skilveg » 01 Fév 2009, 16:27
On a une décomposition de la forme
^2}=\frac{P}{X^n}+\frac{aX+b}{(X-1)^2})
. On calcule

et

comme précédemment, puis on peut expliciter

(et donc ses coefficients).
-
darktitanj
- Membre Naturel
- Messages: 13
- Enregistré le: 17 Jan 2009, 15:43
-
 par darktitanj » 01 Fév 2009, 16:35
par darktitanj » 01 Fév 2009, 16:35
moi je pense que ça te donne 1/(x²) + 1/(x-1)^n
En faite tu fais a/x²+ b/(x-1)^n = 1/(x²(x-1)^n)
Et quand tu multiplies tout par x² et que tu remplaces x par 0 tu obtiens a
et quand tu multiplies tout par (x-1)^n et que tu remplaces x par 1 tu obtiens b
-
darktitanj
- Membre Naturel
- Messages: 13
- Enregistré le: 17 Jan 2009, 15:43
-
 par darktitanj » 01 Fév 2009, 16:36
par darktitanj » 01 Fév 2009, 16:36
enfin c'est la méthode qu'on ma apprise en sciences de l'ingénieur en début d'année
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 01 Fév 2009, 16:39
par skilveg » 01 Fév 2009, 16:39
Je ne pense pas que ce soit cette méthode qu'on t'a appris, vu qu'elle est incorrecte. Il n'y a pas de raison que le numérateur de la fraction en
^n)
soit constant.
D'ailleurs, si ta méthode marchait, on aurait
^n)
: bof.
-
rostand
- Messages: 4
- Enregistré le: 31 Jan 2009, 20:57
-
 par rostand » 03 Fév 2009, 22:21
par rostand » 03 Fév 2009, 22:21
personne ne m'a donné le resultat.mon problème c'est trouver les termes de la somme compliquée :mur:
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 04 Fév 2009, 16:25
par skilveg » 04 Fév 2009, 16:25
Les indications qu'on t'a données devraient te suffire. Dans ce que je raconte il y a quelques posts, tu peux expliciter le numérateur, basiquement par des calculs de sommes géométriques.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
, on multiplie les deux membres de l'égalité par :
, ensuite, on met :
par exemple : et on obtient :
, c'est tellement simple ! il suffit de comprendre le principe et ça ira pour tout le reste ! c'est pas grand chose !
