Théorème :
Soient :
On munit :
Soit :
Les conditions suivantes sont équivalentes :
Questions :
Merci infiniment !
Application multilinéaire continue !
12 messages
- Page 1 sur 1
Application multilinéaire continue !
par barbu23 » 13 Jan 2009, 21:27
Bonjour :
Théorème :
Soient :, ... , (E_n, || . ||_{E_n}) $)
et  $)
des espaces vectoriels normés.
On munit :
de la norme :  || = \max \{ || . ||_{E_1}, ... ,|| . ||_{E_n} \} $)
 $)
est un espace vectoriel normé.
Soit :
une application 
linéaire.
Les conditions suivantes sont équivalentes :
 $)
. 
est continue sur 
.
 $)
. 
est continue seulement en :  $)
.
 $)
. est bornée sur 
, où : 
désigne la boule unité de 
.
 $)
. est bornée sur 
, où : 
désigne la sphère unité de .
 $)
.  \in E_1 \times ... \times E_n $)
:  ||_F \leq \alpha . || x_1 ||_{E_1} ... || x_n ||_{E_n} || $)
Questions :
Comment démontrer :  \Longrightarrow 5) $)
.
Merci infiniment !
Théorème :
Soient :
On munit :
Soit :
Les conditions suivantes sont équivalentes :
Questions :
Merci infiniment !
par Joker62 » 13 Jan 2009, 21:34
Haileau ;)
Pour tout n-uplet de S1xS2x...xSn on a la majoration L(x1,x2,...,xn) <= M
On se donne (x1,...,xn) quelconque dans E1xE2x...xEn on a alors
L(x1/N(x1) , x2/N(x2), ... , xn/N(xn)) <= M
On sort les normes par n-linéarité et on balance de l'autre côté.
Faire attention au cas où un xi serait nul :^)
Pour tout n-uplet de S1xS2x...xSn on a la majoration L(x1,x2,...,xn) <= M
On se donne (x1,...,xn) quelconque dans E1xE2x...xEn on a alors
L(x1/N(x1) , x2/N(x2), ... , xn/N(xn)) <= M
On sort les normes par n-linéarité et on balance de l'autre côté.
Faire attention au cas où un xi serait nul :^)
par barbu23 » 13 Jan 2009, 21:45
Salut "Joker" et bonne année 2009 :
Tout à l'heure, tu as écrit :} , ... , \frac{x_n}{N(x_n)} )\leq M $)
Or : = ... = N(x_n) = 1 $)
car : ils appartiennent tous au cercle unité !
Mais on obtient pas, il y'a quelques choses qui ne va pas dans la démonstration, ou bien peut être, on montre autrement ce théorème !
Est ce que tu sais comment montrer ce théorème ? Ce n'est pas comme ça : \Longrightarrow 2) \Longrightarrow 3) \Longrightarrow 4) \Longrightarrow 5) \Longrightarrow 1) $)
?
Merci infiniment !
Tout à l'heure, tu as écrit :
Or :
Mais on obtient pas
Est ce que tu sais comment montrer ce théorème ? Ce n'est pas comme ça :
Merci infiniment !
par Doraki » 13 Jan 2009, 22:08
barbu23 a écrit:Tout à l'heure, tu as écrit :
Or :
Non il a dit de regarder (x1, ..., xn) quelconques dans E.
Pour prouver 5), on prend un n-uplet quelconque et on cherche à majorer L(x1...xn).
Si aucun xi est nul, on peut dire que xi = (xi / N(xi))*N(xi), pour justement faire apparaître des éléments qui sont sur les sphères pour justement pouvoir appliquer l'hypothèse 4).
par barbu23 » 14 Jan 2009, 12:51
Bonjour :
Je fais en ce moment une petite révision de d'algèbre multilinéaire et continuité, et je bloque dans la démonstration de la propriété suivante :
Propriété :
Soient $)
,  $)
, ... ,  $)
et  $)
des espaces vectoriels normés.
On munit :
de la norme :
|| = \max{ \{ || .||_{E_1} ,...,|| .||_{E_n} \} } $$)
 $)
est un espace vectoriel normé.
Soit :
une application
linéaire.
 $)
.  \in E_1 \times ... \times E_n $)
:  ||_F \leq \alpha . || x_1 ||_{E_1} ... || x_n ||_{E_n} $)
.
 $)
. est continue sur .
Démonstration :
Soit \in E_1 \times ... \times E_n $)
:
Soient
et  \in E_1 \times ... \times E_n $)
:
-L(a_1,...,a_n )=L(a_1+(x_1-a_1),a_2+(x_2-a_2),...,a_n+(x_n-a_n))-L(a_1,...,a_n ) $$)
.  $)
Quelqu'un peut-t-il m'aider à developper par multilinéarité la dernière expression çi-dessus $)
?
Merci infiniment !
Je fais en ce moment une petite révision de d'algèbre multilinéaire et continuité, et je bloque dans la démonstration de la propriété suivante :
Propriété :
Soient
On munit :
Soit :
une application
Démonstration :
Soit
Soient
Quelqu'un peut-t-il m'aider à developper par multilinéarité la dernière expression çi-dessus
Merci infiniment !
par Anneauprincipal » 14 Jan 2009, 13:18
Pour t'aider dans les notations : il suffit de démontrer que L est continue en 0. Et de plus L(a1,...,an)-L(b1,...,bn)=L(a1-b1,...,an-bn).
par Doraki » 14 Jan 2009, 13:26
Non l'application est multi-R-linéaire, pas R^n-linéaire
Et je crois qu'il veut boucler son théorème en montrant 5 => 1 donc 5 => 2 ça lui suffira pas.
Là tu fais apparaître beaucoup trop de termes dans ton calcul.
L'application est multilinéaire donc tu peux faire appraître les (xi-ai) un par un, t'es pas obligé de tous les mettre en même temps.
L(x1...xn) - L(a1...an) = L(x1-a1, x2...xn) + L(a1, x2...xn) - L(a1, a2...an)
et tu continues en faisant pareil variable par variable, etc...
Et je crois qu'il veut boucler son théorème en montrant 5 => 1 donc 5 => 2 ça lui suffira pas.
Là tu fais apparaître beaucoup trop de termes dans ton calcul.
L'application est multilinéaire donc tu peux faire appraître les (xi-ai) un par un, t'es pas obligé de tous les mettre en même temps.
L(x1...xn) - L(a1...an) = L(x1-a1, x2...xn) + L(a1, x2...xn) - L(a1, a2...an)
et tu continues en faisant pareil variable par variable, etc...
par barbu23 » 14 Jan 2009, 14:21
Salut :
Voiçi ce qe j'ai trouvé ( Merci à vous deux pour vos reponses ):
-L(a_1,...,a_n )= \displaystyle \sum_{(z_1,...,z_n) \in \{ a_1 , (x_1 - a_1) \} \times ... \times \{ a_n , (x_n - a_n) \} } L(z_1 , ... , z_n ) - L( a_1, ..., a_n ) $$)
Voiçi ce qe j'ai trouvé ( Merci à vous deux pour vos reponses ):
par barbu23 » 14 Jan 2009, 16:47
Bonjour :
On note : $)
l'espace vectoriel des applications 
linéaires continues.
 $)
, on pose :
 \in { E_{1} \ \{ 0 \} } \times ... \times { E_{n} \ \{ 0 \} } } \frac{ L(x_{1},...,x_{n}) }{ ||x_{1} ||... ||x_{n} || } $)
Question :
Montrer que :
est une quantité qui est bien définie ( i.e : 
) en montrant que :
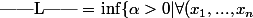 \in E_{1} \times ... \times E_{n} $)
: || \leq \alpha . ||x_{1} || ... ||x_{n} || \} $)
Merci infiniment !!
On note :
Question :
Montrer que :
Merci infiniment !!
par barbu23 » 15 Jan 2009, 12:04
Bonjour :
Quelqu'un connait-t-il la reponse à la question qe je viens de poster çi dessus ?
Merci infiniment !
Quelqu'un connait-t-il la reponse à la question qe je viens de poster çi dessus ?
Merci infiniment !
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :