slt otut le monde voila j'ai ratè le cours dur les applications bijective mais j'essaye tant de mal a les comprendre manque de bol le prof m'a donnè deux exrcises a faire et je sais pas par ou commencer alors si une ame charitable peut m'aider ça serait cool
voila l'exercise
soit f de [0.1[ dans [1.+l'infini[ definin par f(x)= 1/racine carrè de 1-x2
j'esepre que vous imaginer a quoi elle ressemble en global
(1) montrer que f est une application et qu'elle est bijective
(2) definir alors l'application reciproque
soit h la fonction defini sur l'intervalle f= [1.+l'infini[ par f(x)= 4x/x2+1
a/ montrer que h est injective
b/ verifier que quelqusoit x appartenant a f. f(x) est inferieur ou egale a 2
c/ montrer que h est une bijection de f sur ]0.2] et trouver f'(x)
je serais vraiment reconaissant a cleui qui me repondera
Les applications bijectives
8 messages
- Page 1 sur 1
salut,
je plussoie (ou plussie) sur ce qu'écrit Léon1789.
Saurais tu résoudre les deux petits exo suivants ? :zen:
1) un cercle centré à l'origine est-il la courbe représentative d'une fonction ?
2) soit
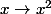
peux tu modifier E et/ou F pour que
f soit injective , non surjective
lui trouver deux inverses à gauche
f soit surjective , non injective
lui trouver deux inverses à droite
f soit bijective
je plussoie (ou plussie) sur ce qu'écrit Léon1789.
Saurais tu résoudre les deux petits exo suivants ? :zen:
1) un cercle centré à l'origine est-il la courbe représentative d'une fonction ?
2) soit
peux tu modifier E et/ou F pour que
f soit injective , non surjective
lui trouver deux inverses à gauche
f soit surjective , non injective
lui trouver deux inverses à droite
f soit bijective
tiens un cours sur les applicatins bijectives:
http://fr.wikipedia.org/wiki/Fonction_(math%C3%A9matiques)
sinon effectivemnet je pense que pour le (1) tu dois montrer que c'est une appli bijective.
http://fr.wikipedia.org/wiki/Fonction_(math%C3%A9matiques)
sinon effectivemnet je pense que pour le (1) tu dois montrer que c'est une appli bijective.
pour prouver que l'application est bijective il faut prouver que la solution de l'équation y=f(x) dans [0.1[ a une seule solution .
aprés resoudre l'equation on trouve qu'elle admet 2 solutions ..
x1 = V(y²-1)/y² ou x2 = - V(y²-1)/y²
on a x appartient à [0.1[ donc x2 n'est pas une solution
on vérifie que x1 appartient à [0.1[
on sait que
quelque soit y appartient à [1.+l'infini[ on a V(y²-1)/y²>=0
1 - V(1 - 1/y² ) = 1 - 1 +1/y² / 1+V(1 - 1/y² ) = 1/(y²(1+V(1 - 1/y² )) > 0
alors y=f(x) admet une seule solution dans [0.1[ qui est
x = V(y²-1)/y²
donc f est bijective
l'application reciproque est f-1 de [1.+l'infini[ vers [0.1[
f-1(x) = V(x²-1)/x²
J'éspere que t'as bien compris et j'attends vos remarques si j'ai commis une faute ..
aprés resoudre l'equation on trouve qu'elle admet 2 solutions ..
x1 = V(y²-1)/y² ou x2 = - V(y²-1)/y²
on a x appartient à [0.1[ donc x2 n'est pas une solution
on vérifie que x1 appartient à [0.1[
on sait que
quelque soit y appartient à [1.+l'infini[ on a V(y²-1)/y²>=0
1 - V(1 - 1/y² ) = 1 - 1 +1/y² / 1+V(1 - 1/y² ) = 1/(y²(1+V(1 - 1/y² )) > 0
alors y=f(x) admet une seule solution dans [0.1[ qui est
x = V(y²-1)/y²
donc f est bijective
l'application reciproque est f-1 de [1.+l'infini[ vers [0.1[
f-1(x) = V(x²-1)/x²
J'éspere que t'as bien compris et j'attends vos remarques si j'ai commis une faute ..
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
