[1ère SSI] DM fonction racine carré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 29 Oct 2008, 11:53
par sylflo » 29 Oct 2008, 11:53
Bonjour à tout le monde.
Voici le lien vers mon DM
http://storage.canalblog.com/71/57/524551/31611915.pdfVoilà j'ai commencé le premier exercice et j'ai calculé le minimum de la fonction racine carré. J'ai trouvé que le minimum de la fonction racine carrré est

sur
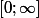
Après je suis complétement bloqué.Je vous remercie d'avance de votre aide.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 29 Oct 2008, 12:03
par rene38 » 29 Oct 2008, 12:03
Bonjour
sylflo a écrit:... j'ai calculé le minimum de la fonction racine carrée.
Tu es hors sujet : on ne demande pas le minimum de la fonction racine carrée mais la valeur de x pour laquelle
la distance AM est minimale.
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 29 Oct 2008, 12:18
par sylflo » 29 Oct 2008, 12:18
Tout d'abord c'est pour vous dire merci de votre réponse.
Je me doutais un peu que ma réponse était fausse mais je dois avouer que là je sais pas du tout quoi faire :mur:.
Et désolé pour la faute de grammaire.
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 29 Oct 2008, 14:53
par sylflo » 29 Oct 2008, 14:53
Bon je sais que je fais un double-post, mais vu que mon message part aux oubliettes et que je suis complètement bloqué.
Donc voilà.Je vous remercie d'avance de votre aide.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 29 Oct 2008, 14:57
par rene38 » 29 Oct 2008, 14:57
Tu as les coordonnées de A.
Quelles sont les coordonnées de M ?
Comment calculer alors AM² (puis AM) ?
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 29 Oct 2008, 15:37
par sylflo » 29 Oct 2008, 15:37
Alors, voilàun début de réponse.
 M(x;y))
Ensuite on a
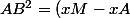^2+(yB-yA)^2<br /> =(x-3)^2+(y-0)^2<br /> =x^2+y^2+9)
C'est juste pour savoir si je suis sur la bonne voie parce que je me demande si il manque pas quelque chose.
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 29 Oct 2008, 18:57
par sylflo » 29 Oct 2008, 18:57
Bon voilà.J'ai passé tout l'après-midi devant ma feuille de math à chercher, j'y arrive pas du tout.Donc c'est pour demander de l'aide s'il vous plaît.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 29 Oct 2008, 19:36
par rene38 » 29 Oct 2008, 19:36
sylflo a écrit:Alors, voilàun début de réponse.

.
Oui mais M est sur la courbe C représentant la fonction racine carrée.
Donc si l'abscisse de M est x alors son ordonnée est ...
Ensuite on a

Mis à part le fait que tu remplaces y par ce que tu viens de trouver ci-dessus,
tu n'aurais pas oublié quelque chose en développant (x-3)² ?
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 29 Oct 2008, 20:25
par sylflo » 29 Oct 2008, 20:25
Alors, j'ai trouvé:
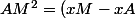^2+(yB-yA)^2<br /> =(x-3)^2+(sqrt{x}<br />-0)^2<br /> =x^2-5x+9)
Ensuite je l'ai mis sous la forme d'un trinôme de second degré.
Ce qui donne
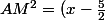^2+\frac{11}{4})
.
Ensuite je suppose qu'on calcule en AM en faisant
racine AM²=(x-5/2)²+11/4 le tout racine
PS:excusez moi mais j'ai pas réussi à mettre l'autre expression en Latex
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 30 Oct 2008, 00:38
par rene38 » 30 Oct 2008, 00:38
La remarque donnée dans l'énoncé :
"
[font=LMRoman10-Italic]La distance [/font][font=LMMathItalic10-Italic]AM [/font][font=LMRoman10-Italic]est minimale si le nombre [/font][font=LMMathItalic10-Italic]AM²[/font][font=LMRoman10-Italic]
est minimal." [/font]
[font=LMRoman10-Italic]
rend inutile le calcul de AM.[/font]
Et le fait d'avoir écrit AM² sous forme canonique te donne la réponse.
NB : "racine AM²=(x-5/2)²+11/4 le tout racine" s'écrit en

AM=\sqrt{AM^2}=\sqrt{(x-\frac{5}{2})^2+\frac{11}{4}}
ce qui donne

-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 30 Oct 2008, 01:45
par yvelines78 » 30 Oct 2008, 01:45
bonsoir,
pour le 2ème, utilise thalès pour calculer MH et aussi que MK=HB=4-x puis calcule l'aire
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 30 Oct 2008, 11:33
par sylflo » 30 Oct 2008, 11:33
Il y a quelque chose que je ne comprend pas pour l'exercice 1 éh oui encore :hum: .
C'est que dans l'énoncé de mon exercice on me dit de déterminer

, mais une fois que j'ai mis
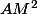
sous forme canonique je dois prouver que la distance est minimale ou bien je calcule

.
Je dois avouer que là c'est le doute totale.
Je vous remercie encore une fois de plus pour l'aide que vous m'apporter. :we:
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 30 Oct 2008, 13:12
par sylflo » 30 Oct 2008, 13:12
Je sais que je suis très embêtant de faire ces doubles post à chaque fois,mais bon au moins j'ai des réponses après,donc voilà je refait remonter le sujet.Vu que ça marche;c'est le résultat qui compte non?
Voilà je vous remercie d'avance.
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 31 Oct 2008, 12:07
par sylflo » 31 Oct 2008, 12:07
Bon voilà c'est pour remonter la discussion parce que là elle été à la 6ème page.Et que l'exercice 1 me pose toujours quelques soucis.
Si des personnes peuvent m'aider,ça serait vraiment sympas de le faire, je vous remercie d'avance.
-
sylflo
- Membre Naturel
- Messages: 61
- Enregistré le: 02 Mai 2008, 11:00
-
 par sylflo » 31 Oct 2008, 15:14
par sylflo » 31 Oct 2008, 15:14
Bon voilà là je commence à craquer. :marteau:
A croire que il y a personne qui puissent m'aider, peut-être que y a personne qui sait faire ça?IL doit bien y avoir quelqu'un qui puissent m'aider.Non? :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 190 invités

 .
.

