[Complexes] Prépas

[FlqX_-]

Salut , voilà on ma posé un problème de prépa , mais je suis en terminale ... Donc je cherche mais si vous pouvez m'aider ça serais cool .Voilà le problème

Résoudre dans P(z)=0
C'est vraiment dur pour moi je trouve rien c'est pas de mon niveau mais il faut absolument que je trouve .
Merci infiniment d'avance , je sais qu'on ne doit pas donner la question comme ça normalement mais mettre son résonnement avant , mais la je cherche mais je doute pouvoir résoudre vu que ce n'est pas de mon niveau c'est pourquoi je demande de l'aide ...

[busard_des_roseaux]

P(2i)=0 d'où P est divisible par z-2i.

[samaie]

Salut , voilà on ma posé un problème de prépa , mais je suis en terminale ... Donc je cherche mais si vous pouvez m'aider ça serais cool .Voilà le problème

Résoudre dans P(z)=0
C'est vraiment dur pour moi je trouve rien c'est pas de mon niveau mais il faut absolument que je trouve .
Merci infiniment d'avance , je sais qu'on ne doit pas donner la question comme ça normalement mais mettre son résonnement avant , mais la je cherche mais je doute pouvoir résoudre vu que ce n'est pas de mon niveau c'est pourquoi je demande de l'aide ...

Ce que tu doit savoir c'est que ce probleme est bien d'un niveau de terminale,ensuite pour ton probleme il suffit de savoir que le degré de ton polynome est 3 et donc il peut s'ecrire sous la forme:
(z-z1)(az²+bz+c)=0
ou z1 est une racine evidente de ton polynome
Comme on te l'a deja dit 2i est racine de ton plolynome est donc il peut s'ecrire sous la forme
(z-2i)(az²+bz+c)=0
Apres avoir fait une identification des coefficient tu trouvera les valeurs de a b et c et tu aura donc a resoudre
(z-2i)=0;
(az²+bz+c)=0;
tu aura finalement la reponse a ta question

[abcd22]

La résolution d'équations du second degré à coefficients complexes n'est pas au programme en terminale, il n'y a que les équations du second degré à coefficients réels, et celles du 3e degré avec une racine évidente sont classiques aussi je suppose.

[busard_des_roseaux]

Tu n'es pas rendu au bout de tes peines:

Il faut calculer le (complexe non réel).

et trouver un (complexe non réel) tel que
.


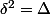
ensuite, on applique les formules habituelles: