Fonction ln . help please

[chipslovee]

bonjour a tous sur ce forum , je suis nouveau

Voici les exos 2 et 3 de mon dm , j'ai reussi a faire lexo mais la je bloque sur les 2 .

merci si quelqu'un peut m'aider !





exo numero 2.

"les premitives de la fonction ln"

1. determinez la derivée de la fonction f definie sur ]0,+infini[ par f(x)=x*ln x
2. en deduire les primitives de la fonction ln sur ]o,+infini[

indiquation : on remarque que ln x = ( ln x + 1 ) - 1




Exo numero 3.

1. determinez un couple (x,y) de nombres reels strictement positifs solution su systeme :

( x+y=9
( ln x + ln Y = ln 14

[armin]

1 )determinez la derivée de la fonction f definie sur ]0,+infini[ par f(x)=x*ln x

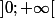
Tu as à dériver une fonction de la forme u*v

Or la dérivée d'une fonction de la sorte est : (uv)' = u'v+uv'

Tu poses u(x) = x et v(x) = ln(x)

Et le tour est joué


Pour la 2 ) :

Utilise le fait que :


Exo numero 3.

( x+y=9
( ln x + ln Y = ln 14

Pour ce systeme utilise le fait que ln a + ln b = ln (a*b) et aide toi de la fonction exponentielle sur l'intervalle

[chipslovee]

merci de ton aide


j'ai pas comprit par contre pour la question 2 exo 2 , et ce que tu m'a dit pour lexo 3.

[armin]

Alors pour la question 2 de l'exo 2 :

Tu cherches une primitive de la fonction ln.
Or on te fait une remarque comme quoi ln(x) = ( ln(x) +1 ) - 1

Tu intégres cette égalité, tu utilises la somme des intégrales et tu trouves si tes calculs sont bons, une primitive de la fonction ln. ( Je sais pas si c'est plus clair ? )

Et pour l'exo 3 :

Il faut que tu utilises le fait que ln (a*b) = ln (a) + ln(b) ( dans ton systeme a =x et b= y )

Et ensuite il faut que tu te souviennes que : tu as

[chipslovee]

ln (a*b) = ln (a) + ln(b) ( dans ton systeme a =x et b= y )

pour ça j'ai comprit .


mais pour l'exo 3 , jai beau chercher et relire , jcomprend vraiment pas

[armin]

Ok Tu veux dire pour l'exo 2 ? avec les intégrales ?

En fait il faut que tu t'aides de la question 1 )

Tu trouves comme dérivée de ta fonction f :
la fonction dérivée suivante :

Ensuite dans ta question 2) On te demande de trouver une primitive de ln(x)
Or tu sais que : ln(x) = ( ln(x)+1 )-1

Ce fameux ln(x)+1 on va l'utiliser !
En effet, si tu consideres une fonction g, définie sur
telle que alors une primitive de cette fonction est :
avec C cste réelle.

Ainsi mtn tu connais une primitive de ln(x)+1 , et je pense que tu n'auras pas de problème à trouver une primitive de la constante 1 :

Par conséquent comme je l'ai dit plus haut.
En utilisant la somme des intégrales tu obtiens :



Mtn vu que tu connais une primitive de ln(x)+1 et de 1 le tour est joué

Tu y es ?

[chipslovee]

enfaite le probleme vient que j'ai pas encore apprit les integrales
.

[armin]

Euh ?
Les intégrales et primitives sont liées :s

Sans passer par le raisonnement que je t'ai dit je vois vraiment pas désolé.

Pourtant tu as qd meme vu que pour tout fonction f, définie et dérivable sur un quelconque intervalle, on note une primitive de f comme suit :

PS : j'viens de penser à un autre truc, car en fait la notation intégrale cest juste une notation ^^

En fait la primitive de la fonction ln(x) notons là H :

Vaut en fait : H(x)= G(x) - C(x)

Avec G(x) une primitive de la fonction g que j'ai définie plus haut
et C(x) qui est une primitive de ta fonction constante

Ceci revient exactement à la meme chose mais sans passer par la notation intégrale

En gros, tu as H(x) = G(x) - C(x) = x ln(x) - x + C = x( ln(x) -1 ) + C , C cste réelle.
Voilà la primitive de la fonction ln

[chipslovee]

oui la prof nous as dit que c'etais lié

mais pour le moment nous ne les avons encore fait

on a fait les primitives , et en ce moment la fonction ln

[Huppasacee]

Pas besoin de te casser la tête avec les intégrales pour la 3

Tu sait ( avec un t ) que lnx + lny = lnxy
Ce qui revient à réécrire l'équation lnxy = ln 14
Or ln est strictement croissante, donc si on cherche un antécédent ......
donc xy = ....
Ensuite, lorsque tu as le produit P et la somme S de 2 nombres, de quelle équation sont ils les solutions ?

[chipslovee]

écrire l'équation lnxy = ln 14

jusqu'a la je te comprend mais pas la suite

[Huppasacee]

Si ln a = ln b alors ..

[chipslovee]

si ln a = ln b

alors

a=b

mais jvois pas en quoi sa nous aide !

:triste: :triste: :triste:

[Huppasacee]

lnxy = ln14
xy = a
14 = b

[chipslovee]

j'ai pas comprit

[Huppasacee]

ln xy = ln 14 donc
xy = 14

Tu as donc le produit P de xy
Tu as leur somme S

Ils sont les solutions de
x²-Sx + P = 0

Ici les solutions sont évidentes

Pour ton exo 1
Si les asmptotes sont -1/2 et 1
alors ax² + bx + c s'annule en ces points
et ln (-b/2a) = ln (5/8 )

[chipslovee]

pourrais tu me rediger la methode a suivre pour lexo 2 stp .

[Huppasacee]

Je reprends l'énoncé :

"les premitives de la fonction ln"

1. determinez la derivée de la fonction f definie sur ]0,+infini[ par f(x)=x*ln x
2. en deduire les primitives de la fonction ln sur ]o,+infini[

indiquation : on remarque que ln x = ( ln x + 1 ) - 1

Fin de citation

C'est souvent que cette méthode est utilisée
on cherche une primitive, on voit intuitivement que cette primitive s'approche d'une fonction qui vient à l'esprit

Ici , c'et x*lnx qui vient à l'esprit

on la dérive et on s'aperçoit que l'on doit juste soustraire un petit quelque chose pour arriver à lnx

on dérive cette cette fonction on trouve lnx + 1 le 1 est en trop

et là on pose
lnx = ( ln x + 1 ) -1
Donc primitive lnx = primitive [lnx + 1 ] - primitive [ 1 ] + Kprim [1] = x

Nous avons vu que prim [ lnx + 1 ] = x*lnx
et
prim [1] = x
donc
primitive de lnx = ....

[Huppasacee]

Dans ma réponse :
et là on pose
lnx = ( ln x + 1 ) -1
Donc primitive lnx = primitive [lnx + 1 ] - primitive [ 1 ] + Kprim [1] = x

la ligne s'arrête à K, le prim [1]=x est en trop

[chipslovee]

jcomprend pas trop ton raisonnement , je suis desolé.. :briques: :briques:

Enfaite j'ai pas envie seulement decrire la reponse sur la feuille , j'ai envie de comprendre.