Tribu
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
parisien75
- Membre Naturel
- Messages: 55
- Enregistré le: 01 Mar 2007, 18:14
-
 par parisien75 » 21 Jan 2008, 21:47
par parisien75 » 21 Jan 2008, 21:47
Bonsoir.
J'ai un exercice sur les tribus qui me pose problème.
Soit

Soit

,

et

.
On me demande de déterminer la tribu engendré par A, B et C :
)
, donc c'est l'ensemble des parties de

que je peux creer à partir de A,B et C par complémentaritée et reunion.
J'obtient ainsi
=(\{vide \};\{1\};\{2\};\{3\};\{1,2\};\{1,3\};\{2,3\};\{1,2,3\};\{1,4,5\};\{2,4,5\};\{3,4,5\};\{1,2,4,5\};\{2,3,4,5\};\{1,3,4,5\};\{ \Omega \}))
On me demande par la suite de caracteriser les applications mesurables de

dans

muni de
})
.
Je ne vois pas trop comment les caracteriser, si vous pouriez me donner une piste,cela m'aiderai !!
Merci d'avance
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Jan 2008, 21:55
par tize » 21 Jan 2008, 21:55
Bonsoir,
essaie une combinaison linéaire des indicatrices de A, B,C et D={3}
-
parisien75
- Membre Naturel
- Messages: 55
- Enregistré le: 01 Mar 2007, 18:14
-
 par parisien75 » 22 Jan 2008, 20:41
par parisien75 » 22 Jan 2008, 20:41
Bonsoir Tize, merci pour ta réponse, mais je ne vois pas trop comment m'y prendre.
A la base, pour montrer qu'une fonction à valeurs dans
}))
est mesurable,on montre que pour tout ouvert

,
)
est mesurable. Et je ne vois pas du tout vers ou me diriger.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Jan 2008, 22:31
par tize » 22 Jan 2008, 22:31
Bonsoir,
déjà tu peux remarquer qu'une partie P est mesurable SSI elle s'écrit comme réunion d'éléments de {A,B,C,D}.
Donc pour tout fermé

,
)
s'écrit comme une réunion d'éléments de {A,B,C,D} et comme f ne peut prendre qu'au plus 4 valeurs a1,a2,a3,a4, et les
)
s'écrivent comme une réunion d'éléments de {A,B,C,D} forcément 2 à 2 disjoints
-
parisien75
- Membre Naturel
- Messages: 55
- Enregistré le: 01 Mar 2007, 18:14
-
 par parisien75 » 23 Jan 2008, 15:42
par parisien75 » 23 Jan 2008, 15:42
Bonjour.
Je ne comprend pas pourquoi on a ceci:
f ne peut prendre qu'au plus 4 valeurs a1,a2,a3,a4
Consideres tu que




Mais pour les autres éléments de

??
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 23 Jan 2008, 15:51
par tize » 23 Jan 2008, 15:51
Bonjour,

n'a que 5 éléments, il y a donc au plus 5 images mais ne fait on peut même dire qu'il y en a au plus 4 car nécessairement
=f(a_5))
car sinon on a par exemple
<f(a_5))
et on pourrait alors trouver un élément de la tribu qui contient
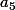
mais pas
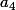
(
;+\infty[\))
) ce qui est impossible d'après la description de la tribu que tu as fait dans ton premier message.
-
parisien75
- Membre Naturel
- Messages: 55
- Enregistré le: 01 Mar 2007, 18:14
-
 par parisien75 » 23 Jan 2008, 17:10
par parisien75 » 23 Jan 2008, 17:10
Donc en reprenant tout:
(

,
)
) un espace mesurable.
On veut caractériser les application mesurable

de

dans
}))
.
On remarque que

prend 5 valeurs au maximum. On les notes

Or, Si on pose
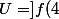;+\infty[)
et on suppose que
<f(5))
alors
)
contient

mais ne contient pas

, donc

n'est pas mesurable sur
))
car
)
nn inclus ds
)
Donc ces application mesurables, possedent 4 images au plusque l'on note :

Mais pourquoi:
et les
)
s'écrivent comme une réunion d'éléments de {A,B,C,D} forcément 2 à 2 disjoints
Pour moi par exemple,
= 1)
Merci pour ta patience .
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 23 Jan 2008, 17:33
par tize » 23 Jan 2008, 17:33
Tout ensemble mesurable est réunion d'éléments de {A,B,C,D} car A,B,C et D sont des éléments constitutifs de la tribu; regarde la tribu que tu as explicitée dans ton message1 tout ensemble mesurable peut s'écrire comme réunion de A, B, C et D.
Pour le "2 à 2 disjoints" c'était dans le cas où l'on a 4 valeurs distinctes....
Mais de manière plus générale (ça se voit, non ?) si
_{i\in I})
forme une partition de

fini telle que tout élément mesurable s'écrit comme réunion de

alors les applications mesurables sont de la forme

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
