Question sur la tribu de Borel sur R

[seriousme]

Bonjour,

la tribu de Borel sur contient tous les ensembles ouverts de .

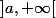
Donc elle contient bien : et ?

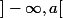
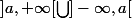
Si oui, alors elle doit aussi contenir (stabilité par union dénombrable), et (stabilité par passage au complémentaire) ?

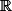
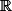
Donc elle doit contenir les singletons de , ce qui n'est à priori pas le cas car sinon elle contiendrait l'ensemble des parties de ce qui est faux .

Où est l'erreur ?

Merci .

[ffpower]

toute partie de R n est pas union denombrable de singletons.ta montré que les ensembles denombrables etaient boreliens la

[seriousme]

Ok, donc le raisonnement est bon, mais la conclusion fausse .

D'ailleurs, les seuls intervalles de de la forme [a,b] étant union dénombrable de singletons sont ceux tels que a = b, non ?

Sinon, quelles sont les parties de ne faisant pas partie de la tribu de Borel :
-
-
... ?

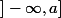
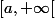
[ThSQ]

Sinon, quelles sont les parties de ne faisant pas partie de la tribu de Borel :
-
-
... ?

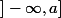
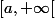
Tout ça en fait partie.

Construire (et imaginer) un ensemble non borélien n'est pas évident ... on en a parler plusieurs fois sur ce forum.

[alavacommejetepousse]

bonjour

il est nécessaire d'utiliser l'axiome du choix

[tito]

bonjour, pour un exemple de partie qui n'est pas un borélien on a:

dans [0,1] on considére la relation d'équivalence : x#y <=> x - y € Q
On "fait le choix" d'un systéme S de représentants des classes d'équivalence de #.(Autrement dit, S est une partie de [0,1] qui contient exactement un seul élément de chaque classe).
Construit de cette façon S n'appartient pas à la tribu borélienne de R
(il est vrai que pour ne pas appartenir à B(R) l'ensemble doit étre particuliérement tourdu :marteau: ces ensembles ce rencontrent particuliérement peu dans les domaines d'applications de la théorie de la mesure que sont le calcul intégral ou encore le calcul de probabilité) :happy2:

A++

[Anonyme]

Bonjour,

la tribu de Borel sur contient tous les ensembles ouverts de .

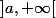
Donc elle contient bien : et ?

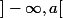
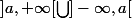
Si oui, alors elle doit aussi contenir (stabilité par union dénombrable), et (stabilité par passage au complémentaire) ?

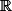
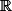
Donc elle doit contenir les singletons de , ce qui n'est à priori pas le cas car sinon elle contiendrait l'ensemble des parties de ce qui est faux .

Où est l'erreur ?

Merci .

Que veux-tu démontrer ?

[seriousme]

Que veux-tu démontrer ?

Rien de particulier, c'était juste pour trouver l'erreur dans le raisonnement .

Merci à tous .

[seriousme]

Finalement, encore une question :

dans [0,1] on considére la relation d'équivalence : x#y x - y € Q
On "fait le choix" d'un systéme S de représentants des classes d'équivalence de #.(Autrement dit, S est une partie de [0,1] qui contient exactement un seul élément de chaque classe).
Construit de cette façon S n'appartient pas à la tribu borélienne de R

N'est-ce pas directement le cas des classes d'équivalences de # ?

En effet pour chaque élément X d'une classe d'équivalence C il n'existe pas de boule centrée sur X appartenant à C : il y aura des nombre réels à une distance irrationnelles de X .

De même le complémentaire de C n'est pas ouvert : il y aura des nombres réels à une distance rationnelle de Y élément de .

?

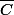
[ThSQ]

il est nécessaire d'utiliser l'axiome du choix

Je crois pas. Pour exhiber un ensemble non mesurable oui.
Un argument de dimension (les Boréliens sont équipotents à IR) suffit ici, mais ça aide peu à les imaginer !

[ffpower]

c ce que je me suis dit aussi,mais ché pas si ya pas besoin de l axiome du choix pour montrer que les boreliens sont equipotents a R..

[alavacommejetepousse]

Je crois pas. Pour exhiber un ensemble non mesurable oui.
Un argument de dimension (les Boréliens sont équipotents à IR) suffit ici, mais ça aide peu à les imaginer !

après réflexion je crois que tu as raison

[ffpower]

mais je veux bien que vous me donniez votre preuve alors car celle que j avais vu se faisait pas reccurence transfinie