Unicité
Olympiades mathématiques, énigmes et défis
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 12 Mai 2007, 09:54
par mt2sr » 12 Mai 2007, 09:54
soit a1,...,an des entiers naturels non tous nuls tel que
)+1=2\prod_{i=1}^{n}(a_i+1))
Montrer qu'il existe un unique i tel que

et dites moi qu'est-ce que vous pensez de mon exercice
j'ai démontré le résultat mais je trouve que ma dem est un peut long j'espère que vous trouviez une plus astisuse est courte
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 12 Mai 2007, 12:42
par aviateurpilot » 12 Mai 2007, 12:42
dsl,
mon erreur ici c'est cette egalité fausse.
=card(\{x|\ x|m\})^2)
je vais posté une autre demo.
 par namfoodle sheppen » 12 Mai 2007, 13:28
par namfoodle sheppen » 12 Mai 2007, 13:28
je pense que tu t'es trompé quelque part parce que pour a1=1 et ai=0 pour i different de 1 l'égalité est vérifié
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 12 Mai 2007, 13:51
par mt2sr » 12 Mai 2007, 13:51
ai<>0 ca vaut dire ai différent de 0
aviateurpilot je crois que vous avez comi une erreur ExE est symétrique donc l'inégalité suivante est incorrecte
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 12 Mai 2007, 14:10
par aviateurpilot » 12 Mai 2007, 14:10
que veux tu dire par

???
soit

(
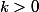
)
soit

avec
_{i=1...n})
des premiers

.
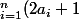+1=2\bigprod_{i=1}^{n}(a_i+1))
equiv à
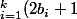+1=2\bigprod_{i=1}^{k}(b_i+1))
equiv à
+1=2d(m))
(
=card(E_x)\ avec\ E_x=\{d>0|\ d|x\})
).
}\in E_{m^2})
on a obtenu donc

diviseur (
}|\ i=1...k\})
) de
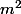
a partir d'un diviseur de

.
donc
\ge k(card(E_{m}))
donc
-1\ge k(d(m))>0)
donc
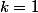
et par suite
+1=2(b_1+1))
=>
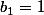
et
=k=1)
concluion: il y a un unique elment non nul

parmi les
_{i=1..n})
qui et egale à

.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 12 Mai 2007, 15:03
par aviateurpilot » 12 Mai 2007, 15:03
soit

(
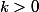
)
soit

avec
_{i=1...n})
des premiers

.
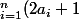+1=2\bigprod_{i=1}^{n}(a_i+1))
equiv à
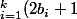+1=2\bigprod_{i=1}^{k}(b_i+1))
equiv à
+1=2d(m))
(
=card(E_x)\ avec\ E_x=\{d>0|\ d|x\})
).

donc

contient

et il est facile de remarquer que
=2d(m)-1=d(m^2)=card(E_{m^2}))
donc

on a

et

donc il exist

(

) tel que

(car

)

donc
=k=1)
concluion: il y a un unique elment non nul

parmi les
_{i=1..n})
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 12 Mai 2007, 23:16
par mt2sr » 12 Mai 2007, 23:16
b1 est quelconque pas forçement 1
-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 13 Mai 2007, 22:25
par redwolf » 13 Mai 2007, 22:25
Mon dieu que c'est compliqué !!!
Aviateurpilot est parti dans la stratosphère !
Prenons un

entier naturel.

Ce quotient est égal à 1 si

et est supérieur à
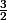
si
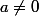
.
Si plus d'un des

est non nul, le produit des quotients correspondants est supérieur à

. C'est une contradiction (l'énoncé prévoit que le produit des

est inférieur à 2).
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 14 Mai 2007, 11:57
par mt2sr » 14 Mai 2007, 11:57
pourquoi >9/4
-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 14 Mai 2007, 13:58
par redwolf » 14 Mai 2007, 13:58
S'il y a deux facteurs supérieurs à
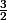
, tous les autres étant supérieurs à 1, le produit est supérieur à
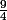
.
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 15 Mai 2007, 14:54
par mt2sr » 15 Mai 2007, 14:54
je crois que la dem de redwolf est invalide
parce que si
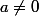
le quotient <=3/2
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 15 Mai 2007, 15:01
par mt2sr » 15 Mai 2007, 15:01
pour l'exercice proposé par yos d(n²)/d(n)=k
l'ensemble k est les entiers impaires reste à prouver ce résultat au donner un contre exemple
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 15 Mai 2007, 15:35
par mt2sr » 15 Mai 2007, 15:35
je crois qu'il faut procéder comme suit
pour k=2p+1 ensuite construire n tel que d(n²)/d(n)=2p+1
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 16 Mai 2007, 17:41
par mt2sr » 16 Mai 2007, 17:41
on pose k=2p+1 alors k+1 est nombre pair on considère t tel

la plus grande puissance de 2 qui divise k+1 et ensuite exprimer

en fonction de t et k (

)
j'arrive pas encore à exprimer les ai mais je suis sûr que c'est une bonne piste
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Mai 2007, 18:44
par Imod » 16 Mai 2007, 18:44
Bonne idée mt2sr , j'ai réussi à conclure que tous les k impairs sont solutions par récurrence en utilisant ton t :++: . Je te ( vous ) laisse chercher encore un peu .
Imod
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 17 Mai 2007, 10:22
par mt2sr » 17 Mai 2007, 10:22
Imod a écrit:
Je te ( vous ) laisse chercher encore un peu .
Imod
j'ai pu le démontrer par récurence j'aimerai savoir comment tu as procédé
je continue à chercher une autre solution sans récurence
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 17 Mai 2007, 11:02
par Imod » 17 Mai 2007, 11:02
On a vu que
}{d(n)})
est impair et
}{d(1)}=1)
. Montrons par récurrence sur

entier positif impair qu'il existe
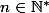
tel que
}{d(n)}=m)
.
Supposons la propriété établie pour

impair et

.
Notons

la valuation 2-adique de
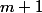
( ie :
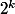
divise
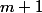
et
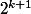
ne divise pas
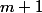
) et
m-1}{2^k}=m-\frac{m+1}{2^k}\in \mathbb{N}})
.
Alors

Or

est entier impair et inférieur à

.
Imod
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 17 Mai 2007, 11:39
par mt2sr » 17 Mai 2007, 11:39
j'ai utilisé le meme x=m-q tel que q le quotient de m+1 par 2^t en utilisant la div euclidienne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités