D(n²)/d(n)

Bonjour,

n est un entier naturel non nul.
On appelle d(n) le nombre de diviseurs positifs de n et d(n²) le nombre de diviseurs positifs de n².

Trouver tous les entiers k>0 pour lesquels il existe un n tel que

d(n²)/d(n)=k.

(Comme vous l'aurez sûrement deviné, c'est un exo d'olympiades :ptdr: )

si n est premier, alors d(n^2)/d(n)=3/2 ? et on se sert de la décomposition en nombre premier de n quelconque ? non?

Si ,
alors et .
D'où , où .
On veut que ce soit un entier, donc les dénominateurs ne peuvent être pairs, donc les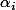 sont pairs ().
On a donc
, où .
En résumé, les entiers cherchés sont les produits d'entiers de la forme g(x), avec x entier.
Quelques essais permettent de conjecturer qu'on obtient tous les nombres impairs. J'ai pas trouvé d'argument pour le prouver.

:++: exactement c'est ce que j'ai trouvé
car j'ai trouvé que n est un carré parfait
et je cherche encore la solution

j'ai trouvé la solution
mais j'ai un petit probleme
c'est coment rediger la demonstration
je vais la posté demain :++:

Bon, j'ai pas trop creusé et je n'ai pas la solution complète.
Voilà une piste naïve :
On note S l'ensemble des entiers naturels qui sont des produits de valeurs de la suite .
En notant I l'ensemble des entiers naturels impairs, on a :. On veut prouver par récurrence que S=I.
On suppose que S contient les entiers 1,3,...,2k-1 et on considère l'entier 2k+1.
Si k est pair, k=2m, on a et , donc et par suite .
Si k est impair, k=2m+1, on a . Si m est pair, on s'en sort comme ci-dessus, et sinon, on doit recommencer en multipliant par 3. Il y a toujours des cas qui restent semble-t-il...

yos,
tu veus que je poste ma soltuion ou t'attendre si tu veus chercher encore

aviateurpilot a écrit:yos,
tu veus que je poste ma soltuion ou t'attendre si tu veus chercher encore

C'est toi qui vois; si je veux chercher, rien ne m'empêche de ne pas regarder.