Inegalite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bankaiyassine
- Membre Naturel
- Messages: 55
- Enregistré le: 29 Mar 2007, 21:34
-
 par bankaiyassine » 24 Avr 2007, 21:56
par bankaiyassine » 24 Avr 2007, 21:56
salut.a et b sot 2 reels strict positifs .demontrer que : b*(1+a^-2)+a*(1+b^-2)>=4 .merci
-
bankaiyassine
- Membre Naturel
- Messages: 55
- Enregistré le: 29 Mar 2007, 21:34
-
 par bankaiyassine » 24 Avr 2007, 22:23
par bankaiyassine » 24 Avr 2007, 22:23
ya personne pour repondre

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 24 Avr 2007, 23:29
par nuage » 24 Avr 2007, 23:29
Salut,
Prend
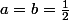
[modification] mes excuses, j'ai mal lu l'énoncé.
 par hamza_mounim » 24 Avr 2007, 23:35
par hamza_mounim » 24 Avr 2007, 23:35
c'est très facile mon petit bankai hhhhhhhhhhhhhhhh
yassine si tu veu la solution donne moi 200dh hhhhhhhhhh
pour les autres c gratwi
 par sandrine_guillerme » 24 Avr 2007, 23:58
par sandrine_guillerme » 24 Avr 2007, 23:58
Je ne comprends pas trop ce qui t'excite, mais si t'es là pour te moquer des gens, ça m'étonerais que tu sois le bienvenue parmi nous,
Calme un tit peu ta joie ,et va l'exprimer ailleurs stp ..
D'avance Merci
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 25 Avr 2007, 08:41
par alben » 25 Avr 2007, 08:41
Bonne journée,
On peut toujours faire l'étude de la fonction et chercher pour quelles valeurs de (a,b) les dérivées s'annulent. Il n'y a qu'un seul couple (1,1).
Mais il existe sans doute une méthode plus directe
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Avr 2007, 11:32
par yos » 25 Avr 2007, 11:32
Bonjour.
En posant x=1/a, y=1/b, on est ramené à prouver que

. Mais

et

, et c'est fini car
\geq 2\times 2xy)
.
A vérifier.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 25 Avr 2007, 14:13
par Imod » 25 Avr 2007, 14:13
Bonjour yos , j'étais arrivé à la même chose en remarquant que pour

,
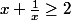
or :
+a(1+\frac{1}{b^2})=\frac{b}{a}(a+\frac{1}{a})+\frac{a}{b}(b+\frac{1}{b})\geq 2.(\frac{b}{a}+\frac{a}{b})\geq 4.)
Imod
PS : coquille corrigée
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Avr 2007, 14:47
par yos » 25 Avr 2007, 14:47
Bonjour Imod.
C'est bien vu.
Une coquille à corriger.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
