Trouve pas les mêmes résulats que l'ennoncé : règles de bioc
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 03 Mar 2007, 19:22
par pouik » 03 Mar 2007, 19:22
Bonsoir,
J'ai essayé avec de nombreuses personnes de résoudre ce micro exercice, mais sans succès : je ne trouve pas les résultats donnés par le texte. Y a t une faute d'ennoncé ou est-ce moi ?? Merci d'avance pour votre aide.
On souhaite calculer en fonction du réel

l'intégrale
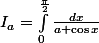
.
i. Justifier l'existence de ces intégrales.
Je ne vois pas : car pour moi avec a définie comme ceci, le dénominateur peut s'annuler.ii. En effectuant le changement de variable
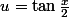
, établir :
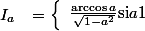
 par Daragon geoffrey » 03 Mar 2007, 21:49
par Daragon geoffrey » 03 Mar 2007, 21:49
slt pour un intervalle de u correct en locurrence xds ]-pi/4;pi/4[, le chgt de variable u=tan(x/2) equiv à x=2arctan(x), implique dx=2/(1+u2)du ce qui donnne lexpression en fct de u : 2/[u^2(a-1)+a+1)] il s'agit alors de decomposer cette fraction en element simple : si a>1, le denominateur se factorise en (u*rac(a-1)+rac(a+1))*(u*rac(a-1)-rac(a+1))... on cherche alors deux reels c et d tels que c/(u*rac(a-1)+rac(a+1)) + d/(u*rac(a-1)-rac(a+1)) = 2/... procede par identifiction tu dois trouver (sauf ereur dema part) d=-1/ra(a+1) et c=-d !!! j'te laisse poursuivre, après simplification tu retombes bien surles expressions proposées @ +
 par Daragon geoffrey » 03 Mar 2007, 21:53
par Daragon geoffrey » 03 Mar 2007, 21:53
oui j'y pense ces intgrales existent car les fonctions de ce type sont clairement continues et meme derivable sur leur intervalle de definition, pour le verifier tu eux les etudier rapidement, les valeurs de a pour lesquels le denominateur sannule sont ds [-1;1] il te suffit donc de prendre a ds ]1;+inf[ par exemple !
@ +
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Mar 2007, 23:05
par yos » 03 Mar 2007, 23:05
Bonsoir.
Je pense comme Pouik qu'il faut a>0.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 04 Mar 2007, 10:21
par pouik » 04 Mar 2007, 10:21
Bonjour,
Merci pour vos réponses.
Pourriez vous etre un peu plus clair sur le calcul des intégrales car moi je trouve des intégrales en arctan... :marteau:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 04 Mar 2007, 10:50
par pouik » 04 Mar 2007, 10:50
Daragon Goeffroy, si on prend

, alors comment traite-on le cas
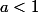
?? :hum: :hum:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 04 Mar 2007, 11:12
par pouik » 04 Mar 2007, 11:12
mais il y a un petit problème dans ce que vous me proposez car :
(u*rac(a-1)+rac(a+1))*(u*rac(a-1)-rac(a+1)) n'est pas égal à 2/[u^2(a-1)+a+1)] mais à 2/[u^2(a-1)-a-1)]
Comment faire ?? je suis perdu... :mur: :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
