Bonjour,
La question est de déterminer le module et un argument de Z.
Je trouve module de Z = 1
Argument de Z = arctan (-sin¢/cos¢) - arctan(-cos¢/sin¢)
Est ce juste ?
Z=(cos¢-isin¢) /(sin¢-icos¢)
12 messages
- Page 1 sur 1
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
Bonsoir,
|
-isin(\alpha)}{-i(cos(\alpha)+isin(\alpha))})
=-\alpha-(-\dfrac{\pi}{2})-\alpha)
=-2\alpha+\dfrac{\pi}{2}[2\pi])
|
Modifié en dernier par mathelot le 02 Nov 2022, 22:26, modifié 3 fois.
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
Pour rapprocher ton résultat du mien,on a les égalités:
arctan(-x)=-arctan(x)
Pour x>0
arctan(1/x)= /2 - arctan(x)
/2 - arctan(x)
Pour x<0
arctan(1/x)=- /2-arctan(x)
/2-arctan(x)
arctan(-x)=-arctan(x)
Pour x>0
arctan(1/x)=
Pour x<0
arctan(1/x)=-
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
Bonjour,
Merci encore pour ta réponse.
Mais je vois pas comment tu arrives à ce résultat.
Malgré ton explication sur les égalités.
Est ce possible de me détailler plus, pour que je comprenne ?
Dois Je comprends que mon résultat est totalement faux ou pas simplifier ?
Cordialement
Merci encore pour ta réponse.
Mais je vois pas comment tu arrives à ce résultat.
Malgré ton explication sur les égalités.
Est ce possible de me détailler plus, pour que je comprenne ?
Dois Je comprends que mon résultat est totalement faux ou pas simplifier ?
Cordialement
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
Re,
Je trouve une réponse avec arctan car j'applique la formule du cours pour trouver l'argument Z: theta=arctan (b/a)
Je trouve une réponse avec arctan car j'applique la formule du cours pour trouver l'argument Z: theta=arctan (b/a)
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
Z=\frac{(\cos \alpha - i\sin \alpha )}{(\sin \alpha - i\cos \alpha)}\P
\P
Z1 = \cos \alpha - i\sin \alpha\P
Z2 = \sin \alpha - i\cos \alpha\P
\P
Calcul du module de Z1:
module de Z1 = \sqrt{(\cos \alpha)^{2} + (-i\sin \alpha)^{2}}\P
module de Z1 = \sqrt{(\cos ^{2} \alpha) + i\sin ^{2}\alpha)^{2}}\P
module de Z1 = \sqrt{1}\P
module de Z1 = 1 \P
\P
module de Z2 = \sqrt{(\sin \alpha)^{2} + (-i\cos \alpha)^{2}}\P
module de Z1 = \sqrt{(\sin ^{2} \alpha) + i\cos ^{2}\alpha)^{2}}\P
module de Z1 = \sqrt{1}\P
module de Z1 = 1 \P
\P
module de Z = \frac{Z1}{Z2}\P
module de Z = \frac{1}{1}=1\P
\P
\arg Z = \arg Z1 - \arg Z2\P
\P
\arg Z1 = arctan \frac{(-\sin\alpha)}{\cos\alpha }\P
\arg Z1 = -arctan frac{(\sin\alpha)}{\cos\alpha } = arctan (tan \alpha )\P
\P
\P
\arg Z2 = arctan \frac{(-\cos\alpha)}{\sin\alpha } = - arctan \frac{\cos\alpha)}{\sin\alpha}\P
\P
donc \arg Z = arctan (tan \alpha )- (- arctan \frac{\cos\alpha)}{\sin\alpha})\P
\arg Z = arctan (tan \alpha )+ arctan \frac{\cos\alpha}{\sin\alpha}\P
\P
Z1 = \cos \alpha - i\sin \alpha\P
Z2 = \sin \alpha - i\cos \alpha\P
\P
Calcul du module de Z1:
module de Z1 = \sqrt{(\cos \alpha)^{2} + (-i\sin \alpha)^{2}}\P
module de Z1 = \sqrt{(\cos ^{2} \alpha) + i\sin ^{2}\alpha)^{2}}\P
module de Z1 = \sqrt{1}\P
module de Z1 = 1 \P
\P
module de Z2 = \sqrt{(\sin \alpha)^{2} + (-i\cos \alpha)^{2}}\P
module de Z1 = \sqrt{(\sin ^{2} \alpha) + i\cos ^{2}\alpha)^{2}}\P
module de Z1 = \sqrt{1}\P
module de Z1 = 1 \P
\P
module de Z = \frac{Z1}{Z2}\P
module de Z = \frac{1}{1}=1\P
\P
\arg Z = \arg Z1 - \arg Z2\P
\P
\arg Z1 = arctan \frac{(-\sin\alpha)}{\cos\alpha }\P
\arg Z1 = -arctan frac{(\sin\alpha)}{\cos\alpha } = arctan (tan \alpha )\P
\P
\P
\arg Z2 = arctan \frac{(-\cos\alpha)}{\sin\alpha } = - arctan \frac{\cos\alpha)}{\sin\alpha}\P
\P
donc \arg Z = arctan (tan \alpha )- (- arctan \frac{\cos\alpha)}{\sin\alpha})\P
\arg Z = arctan (tan \alpha )+ arctan \frac{\cos\alpha}{\sin\alpha}\P
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
après remise en forme et je pense à quelques modifications à partir d' un argument de 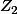



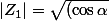^{2} + (-i\sin \alpha)^{2}})
 + i\sin ^{2}\alpha)^{2}})

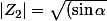^{2} + (-i\cos \alpha)^{2}})
 + i\cos ^{2}\alpha)^{2}})



 = \arg( Z_1) - \arg( Z_2))
 = arctan \dfrac{(-\sin\alpha)}{\cos\alpha })
 = -arctan (\dfrac{\sin\alpha}{\cos\alpha }) =- arctan (tan (\alpha )))
 = arctan (\dfrac{-\cos\alpha}{\sin\alpha }) = - arctan[tan(\dfrac{\pi}{2}-\alpha)]})
 = -arctan (tan \alpha )+arctan[tan(\dfrac{\pi}{2}-\alpha)]})
)=x\, ssi \, x\in\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right])
 = \dfrac{\pi}{2}-\alpha-\alpha)
Re: Z=(cos¢-isin¢) /(sin¢-icos¢)
rebonjour,
Je vois où j'ai bloqué, mais je comprends pas comment vous arrivez à passer de :
arg(z2)= arctan(-cosx/sinx) = -arctan(tan(pi/2-x)
Je ne comprends pas cette transition, qui est le plus important de l'exercice.
Sinon, dans mon brouillon je n'avais pas mis le i pour le calcul du module.
Merci pour vos réponses.
Je vois où j'ai bloqué, mais je comprends pas comment vous arrivez à passer de :
arg(z2)= arctan(-cosx/sinx) = -arctan(tan(pi/2-x)
Je ne comprends pas cette transition, qui est le plus important de l'exercice.
Sinon, dans mon brouillon je n'avais pas mis le i pour le calcul du module.
Merci pour vos réponses.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
