Bonjour,
Uo=8 et U(n+1)=Racine(Un + 1)
Démontrer par récurrence : 1<=U(n+1)<=Un
Initialisation: U1=3
1<=3<=8 donc vrai
Soit Pn: 1<=U(n+1)<=Un. Il faut démontrer : 1<=U(n+2)<=U(n+1)
Je pars de Pn car supposée vraie.
1<=U(n+1)<=Un
1<=Racine(Un +1)<=Un
1<=U(n+1 )<=Un
Là je bloque.
Merci d'avance
Récurrence
9 messages
- Page 1 sur 1
Re: Récurrence
Bonjour
Partir de la double inégalité qui est l'hypothèse de récurrence puis lui appliquer successivement les deux fonctions suivantes en précisant leur sens de variation :

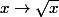
Partir de la double inégalité qui est l'hypothèse de récurrence puis lui appliquer successivement les deux fonctions suivantes en précisant leur sens de variation :
Re: Récurrence
f(x)=Racine(x+1) définie sur [-1;+oo[
f'(x)=1/(2Racine(x+1) sur]-1;+oo[
f'(x)> 0 sur ]-1;+oo[
Donc f strictement croissante sur [-1;+oo[
f(1)<=f(U(n+1))<=f(Un)
1<=Racine(2)<=U(n+2)<=U(n+1) puis la phrase habituelle de l'hérédité.
C'est ça ?
f'(x)=1/(2Racine(x+1) sur]-1;+oo[
f'(x)> 0 sur ]-1;+oo[
Donc f strictement croissante sur [-1;+oo[
f(1)<=f(U(n+1))<=f(Un)
1<=Racine(2)<=U(n+2)<=U(n+1) puis la phrase habituelle de l'hérédité.
C'est ça ?
Re: Récurrence
Oui c'est correct .
f a simplement besoin d'être strictement croissante sur [1;+oo[ donc pas la peine de s'embêter avec la valeur (-1) où f n'est pas dérivable.
f a simplement besoin d'être strictement croissante sur [1;+oo[ donc pas la peine de s'embêter avec la valeur (-1) où f n'est pas dérivable.
Re: Récurrence
Méthode ? Là je vois plutôt que tu tournais en rond !
Il y a d'autres méthodes mais celle là est la plus rapide.
Il y a d'autres méthodes mais celle là est la plus rapide.
Re: Récurrence
Oui, je tournais en rond.
Peux-tu m'en donner une ?
"Il y a d'autres méthodes mais celle là est la plus rapide."
Peux-tu m'en donner une ?
Re: Récurrence
Par ex;
Poser f définie sur R+ par=\sqrt{x+1})
On a)
donc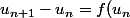-u_n)
Une étude du signe de f(x)-x permet de conclure pour le sens de variation de la suite, mais dans cet exemple c'est mal adapté.
Poser f définie sur R+ par
On a
donc
Une étude du signe de f(x)-x permet de conclure pour le sens de variation de la suite, mais dans cet exemple c'est mal adapté.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
