Changement d'indice somme

[ayle]

bonjour je reposte le sujet en photo
je bloque à partir de la question 4 ou il faut remarquer que An s'ecrit d'une autre maniere
j'ai posé p=3k mais je ne comprends pas comment on arrive à p allant jusqu'a 3n+2 dans la nouvelle expression

merci

[infernaleur]

Salut,
Si , alors donc on le compte pas.
Si , alors donc on le compte pas.

Donc tu peux les rajouter ça change rien.

[ayle]

Salut,
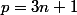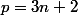Si , alors donc on le compte pas.
Si , alors donc on le compte pas.

Donc tu peux les rajouter ça change rien.

je suis pas sur d'avoir compris
juste quand je fais mon changement d'indice, je pose p=3k
donc logiquement lorsque n=k : p=3n et non 3n+2

[infernaleur]

Oui tu peux écrire la somme de 0 jusqu'a 3n, c'est vrai, mais pour faire la somme An+Bn+Cn dans la question suivante ça sera mieux d'écrire la somme jusqu’à 3n+2.

En gros ta somme elle demande deux conditions, que p soit compris entre 0 et 3n et que p soit divisible par 3.
Si l'une des deux conditions n'est pas vérifié le p tu le prend pas. Donc comme 3n+1 et 3n+2 ne sont pas divisible par 3 tu peux les rajouter (de toute façon tu les prendras pas en compte comme ils rentrent pas dans les deux conditions)

[ayle]

ok super merci j'ai compris pour ça et pour la somme An+Bn+Cn c'est bizarre parce qu'il faudra à la fois que p soit congru à 0 modulo 3,p congru à 1 modulo 3 et p congru à 2 modulo 3 si on pose pour Bn p=3k+1 et pour Cn p=3k+2?

[infernaleur]

Oui tu fais la même chose pour Bn et Cn et tu obtiens 3 même somme les seuls choses qui différent c'est




Après tu as donc

[ayle]

Oui tu fais la même chose pour Bn et Cn et tu obtiens 3 même somme les seuls choses qui différent c'est




Après tu as donc

si on obtient les mêmes sommes pourquoi on obtient pas 3 fois ce résultat

[ayle]

okkkkk d'accord non ok j'ai compris c'est de l'arithmetique on obtient tous les p

[infernaleur]

J'ai pas dit qu'on obtenait les mêmes relis bien.

L'indexation de p n'est pas la même pour les trois sommes.
Mais quand on les additionne ça donne la somme complète parce que pour un entier p tu as que 3 cas :
soit il est congru à 1 modulo 3, soit à 2 , soit à 3.

[ayle]

J'ai pas dit qu'on obtenait les mêmes relis bien.

L'indexation de p n'est pas la même pour les trois sommes.
Mais quand on les additionne ça donne la somme complète parce que pour un entier p tu as que 3 cas :
soit il est congru à 1 modulo 3, soit à 2 , soit à 3.

ok j'ai compris merci beaucoup je vais essayer de faire la suite tout seul

[ayle]

Oui tu fais la même chose pour Bn et Cn et tu obtiens 3 même somme les seuls choses qui différent c'est




Après tu as donc

mais enfaite ducoup cette somme la c'est 2^3n+2 d'après la formule du binome de newton je crois non

[infernaleur]

oui si tu parenthèse mieux ton expression

[ayle]

question 7 pas simple aussi

[ayle]

je trouve 0 pour la 7 je sais pas si c'est normal?

[infernaleur]

Tu peux prendre le conjugué pour la 7), mais sinon c'est exactement comme la question d'avant sauf qu'a au lieu d'avoir des j tu as des j²