Forumule Cauchy pour les séries entières
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MoonX
- Membre Naturel
- Messages: 85
- Enregistré le: 30 Oct 2016, 22:39
-
 par MoonX » 24 Déc 2018, 12:35
par MoonX » 24 Déc 2018, 12:35
Bonjour,
Pour une série entière
 = \sum a_n z^n)
de rayon de converge infini.
Je dois établir pour
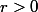
:
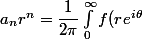e^{-in\theta}d\theta)
Je suis dubitatif... Je sais le montrer pour l'intégrale s'arrêtant à 2pi, mais si elle va jusqu'à l'infini, elle est censée diverger non ? (par périodicité, c'est comme si on sommait une infinité de termes non nuls ?)
Ou alors je passe à coté d'un truc basique qui ne me vient pas à l'esprit, ou bien il est implicite que ça s'arrête à 2pi, ou bien l'énoncé est faux.... Dans tous les cas, j'aimerai m'assurer de bien tout comprendre.
Je vous remercie par avance !
-
aviateur
 par aviateur » 24 Déc 2018, 12:50
par aviateur » 24 Déc 2018, 12:50
l'énoncé est bien sûr faux. Si c'est 0 à 2pi c'est pas de 0 à l'infini!!!!
Et la formule est une conséquence immédiate du th des résidus. Si il y a une démo à faire c'est donc le th des résidus.
-
MoonX
- Membre Naturel
- Messages: 85
- Enregistré le: 30 Oct 2016, 22:39
-
 par MoonX » 24 Déc 2018, 13:10
par MoonX » 24 Déc 2018, 13:10
Merci beaucoup pour cette réponse !
Je n'ai pas le théorème des résidus (le programme de prépa ne s'aventure malheureusement pas en analyse complexe), mais ça se montre facilement avec les théorèmes d'inversion de somme et d'intégrale.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
