Cryptage arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 29 Oct 2018, 23:46
par mehdi-128 » 29 Oct 2018, 23:46
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Oct 2018, 14:03
par mehdi-128 » 30 Oct 2018, 14:03
Je ne comprends pas comment on obtient le résultat suivant :
Il n'existe aucun
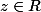
tel que :
=2)
pour
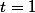
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 30 Oct 2018, 19:22
par pascal16 » 30 Oct 2018, 19:22
x² modulo 29 ne peut pas être congrue à 2.
c'est comme en base 10, un carré ne peut pas finir par n'import quel chiffre
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Oct 2018, 19:54
par mehdi-128 » 30 Oct 2018, 19:54
pascal16 a écrit:x² modulo 29 ne peut pas être congrue à 2.
c'est comme en base 10, un carré ne peut pas finir par n'import quel chiffre
Comment le démontrer ? Je pense qu'il faut utiliser le 28 divise

mais je vois pas exactement.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 30 Oct 2018, 20:36
par pascal16 » 30 Oct 2018, 20:36
j'ai pris le tableur et hop
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 30 Oct 2018, 23:32
par mehdi-128 » 30 Oct 2018, 23:32
D'accord mais je cherche à le démontrer

D'après la propriété 2) soit

et

Il existe alors un
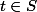
tel que :
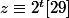
et

(x=1)
Toujours d'après 2) :
=2 \Leftrightarrow z^k \equiv 2 [29] \Leftrightarrow 28 |(kt-1))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités