Question réduction de matrice

[Abilys38]

Bonjour,

Je suis en train de réaliser un exercice dans lequel je dois déterminer l'ensemble des matrices M de M3(R)
telles que M² = A.

Voilà le procédé:

Diagonaliser A

Recherche des valeurs propres de A ==> Fait
Recherche des espaces propres de A ==> Fait
On a ensuite une matrice avec les trois colonnes de sous espaces propres (P) ==> Fait
On inverse cette matrice ==> Fait
On diagonalise A en faisant P^-1 A P ==> Fait

Ma question:

La dernière étape, c'est de déterminer la matrice diagonale de M qui est simplement l'ensemble des racines
de la matrice diagonale de A, puis on détermine M (voir photo).
Ce que je ne comprend pas, c'est:

Pourquoi M était forcément diagonalisable?
Il me manque, je pense, quelques propriétés fondamentales. Je ne comprend du coup pas le corrigé de la photo.
Pour info, la matrice A de départ est:

1 3 0
3 -2 -1
0 -1 1

Merci beaucoup!!

[Elias]

Salut,

Je pense que la question que l'on doit d'abord se poser est: pourquoi y'a t-il unicité d'une matrice M vérifiant M^2=A dans cette situation.
C'est ce que tu sous entend lorsque tu demandes "pourquoi M est-elle forcément diagonalisable". Ou alors il aurait fallut poser la question "pourquoi toute solution est elle forcément une matrice diagonalisable".

Ici, A est une matrice symétrique, tu as donc pu la diagonaliser et ses valeurs propres etaient positives, tu as donc pu trouver avec le procédé que tu décrit une matrice M diagonalisable solution.

Ensuite, ici l'unicité est dû notamment au fait que si M est solution, alors M commute avec A et l'endomorphime associé stabilise les espaces propres de A mais je ne sais pas trop si tu as connaissance de ces résultats.

PS: la photo du corrigé n'est pas disponible. Est ce que l'unicité etait abordée ou pas ?

[Ben314]

Salut,
J'ai pas tout capté des tenant et aboutissant du bidule, mais ça :

...pourquoi y'a t-il unicité d'une matrice M vérifiant M^2=A dans cette situation.

ça me semble faux de chez faux : rien qu'en dimension 1 (i.e. avec des matrices 1x1, c'est à dire des scalaires) c'est déjà faux : pour a fixé, l'équation x²=a admet deux solution dans R si a>0 et aucune si a<0.

Sinon, le fait que LES (et pas LA) racineS carréeS d'une matrice diagonale sont forcément diagonales, c'est, à mon sens, pas du tout une évidence et c'est même faux si on ne suppose pas que la matrice diagonale de départ (dont on cherche les racines carrées) est à valeur propre distinctes.
Par exemple, la matrice (diagonale) admet comme racine carrées non seulement les 4 matrices (diagonales), mais aussi toutes celle de la forme (non diagonales).

[Abilys38]

Justement, ce que j'aimerais comprendre, c'est pourquoi ici, toutes les racines de la matrice diagonale sont des matrices diagonales.

Trident, justement, je n'en ai pas connaissance mais je veux en avoir connaissance !! Car ça m'aidera à justifier la réponse. Mais c'est un DM de niveau L1 avec pour moi quelques propriétés de niveau L2 (réduction endomorphisme)

Il y a un bug et le fichier ne s'ajoute pas "desolé mais le quota a été atteint".

[Ben314]

Le plus simple, je pense que c'est effectivement d'utiliser ça :

...l'endomorphime associé stabilise les espaces propres de A mais je ne sais pas trop si tu as connaissance de ces résultats.

Soit une matrice diagonale avec 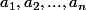distincts dans la diagonale. On cherche les matrices qui commutent avec , c'est à dire telles que .
Si on note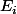 le i-ième vecteur (colonne) de la base canonique (avec que des 0 sauf un 1 en i-ième position) alors donc, si , on doit avoir ce qui signifie que le vecteur vérifie c'est à dire qu'il est dans le sous-espace propre associé à la valeur propre . Or, vu que les sont distinct, le sous espace propre associé à il est de dimension 1 et engendré par l'unique vecteur 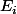donc en fait pour un certain (*) c'est \`a dire ce qui signifie que la i-ième colonne de la matrice c'est avec le en i-ième position.
Et vu que c'est vrai pour tout , ça prouve bien que la matrice est diagonale.

Ensuite, concernant les racines carrées de , il suffit de constater que, si est une racine de , c'est à dire si alors on a donc commute avec et donc, si est diagonale avec des valeurs distinctes sur la diagonale, alors est diagonale.
Et c'est clair que les valeur sur la diagonale de D, ce sont des racines carrées de celles de donc, si on reste dans R, pour que A admette des racines carrées, il faut que tout les soient positifs et le nombre de racines carrées de A, ça va être 2^n si les sont tous strictement positifs (ils ont donc tous deux racines carrés dans R) ça va être 2^(n-1) si un des est nul et les autres sont strictement positifs (le réel 0 n'a qu'une seule racine carrée)

(*) A la limite, si la notion de sous espace propre c'est pas trop clair pour toi, tu peut parfaitement écrire que (en colonne) et vérifier "à la main" que les solutions du système linéaire c'est bien les , c'est à dire que tout les 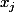doivent être nuls, sauf qui lui peut être égal à n'importe quoi.

[Abilys38]

Si, c'est trés clair et m'a bien aidé à comprendre !! Merci beaucoup !!

[Elias]

Salut,
J'ai pas tout capté des tenant et aboutissant du bidule, mais ça :

...pourquoi y'a t-il unicité d'une matrice M vérifiant M^2=A dans cette situation.

ça me semble faux de chez faux

Oui, c'est bien sûr faux dans le cas général mais je m'interrogeais par rapport au corrigé dans le cas particulier de la matrice de Abilys38 :
1 3 0
3 -2 -1
0 -1 1

Ici, ce qui a été fait dans le corrigé, c'est simplement trouver une solution particulière de l'équation M^2=A mais elle n'a pas été résolue puisque résoudre cette équation, c'est trouver toute(s) le(s) matrice(s) solution(s).


Dans mon histoire d'unicité, je faisais référence au résultat qui dit que si A est une matrice symétrique positive, alors il existe une unique matrice M symétrique positive telle que M^2=A.

[Abilys38]

Par contre, maintenant, revenons au problème de départ. A n'est au départ pas diagonale, et je cherche les M tel que M² = A. Je recopie le processus du premier message:

Diagonaliser A dans un premier temps

Recherche des valeurs propres de A ==> Fait
Recherche des espaces propres de A ==> Fait
On a ensuite une matrice avec les trois colonnes de sous espaces propres (P) ==> Fait
On inverse cette matrice ==> Fait
On diagonalise A en faisant P^-1 A P ==> Fait

Ma question, c'est: Pourquoi M est elle aussi diagonalisable?
On vient de démontrer que si A est diagonale et que M commute avec A, M est diagonale.
J'aimerais maintenant comprendre: A est diagonalisable, et M commute avec A, donc M est diagonalisable?

Voilà le passage du corrigé que je ne comprend pas.

Soit M une matrice deM3(C) solution de M² = A . M et A commute, A est diagonalisable : les sous-espaces
propres de A sont stables par M, M est donc diagonalisable dans la même base que A.

[Ben314]

Si c'est effectivement écrit texto que "M est diagonale" dans ton corrigé, effectivement, c'est faux.
Au départ, tu cherchais une solution de M² = A.
Ensuite, tu as montré que D = P^-1 A P est une matrice diagonale.
Arrivé à ce point, ce qu'il faut faire, c'est le même changement de base sur la matrice M, c'est à dire considérer la matrice N = P^-1 M P.
On a donc A = P D P^-1 et M = P N P^-1 donc l'équation M²=A s'écrit (P N P^-1)²=P D P^-1 qui, après simplification, donne (évidement) N² = D.
Et c'est là que tu peut affirmer que, vu que N est une racine carrée de la matrice diagonale (et à valeur propres distinctes) D, c'est qu'elle est elle même diagonale (en bref, c'est pas M qui est diagonale, c'est N = P^-1 M P).

Sinon, ça :

Soit M une matrice deM3(C) solution de M² = A . M et A commute, A est diagonalisable : les sous-espaces
propres de A sont stables par M, M est donc diagonalisable dans la même base que A.[/b]

ben c'est très exactement ce que je t'ai détaillé dans le post précédent (modulo que je trouve que dans la phrase en question, il manque drastiquement la précision indispensable que les s.e.v. propres de A sont supposés être tous de dimension 1)

[Pseuda]

Voilà le passage du corrigé que je ne comprend pas.
Soit M une matrice deM3(C) solution de M² = A . M et A commute, A est diagonalisable : les sous-espaces
propres de A sont stables par M, M est donc diagonalisable dans la même base que A.

Bonjour,

Supposons que et commutent. Si est un sous-espace propre de associé à la valeur propre , et si , alors , donc , donc appartient à .

Ainsi, est stable par : .
Je n'ai pas fait les calculs : est-ce que les sous-espaces trouvés sont des droites vectorielles ? Si oui, Les sous-espaces de M sont ceux de A, et donc M est diagonalisable dans la même base que A.

Pas vu le message de Ben314.

[Abilys38]

Merci pour vos réponses.

Effectivement Ben, il y avait donc un moyen simple de montrer cela...

Pseuda, je confirme que les sev sont des droites. Donc il me semble, comme Ben la montre plus haut, que les vecteurs propres de A le sont aussi pour M.

[Pseuda]

Oui (vois-tu pourquoi ?), et les valeurs propres de M sont (si elles existent) les racines carrées des valeurs propres de A (on peut le montrer en calculant si est un vecteur propre de associé à la valeur propre , et de M associé à .)

[Elias]

Personne ne parle à aucun moment de l'équation M^2=A.
Elle n'a pour moi toujours pas été résolue.
Quel est l'ensemble solution de cette équation du coup ???

Et puis pourquoi on parle de matrices diagonales depuis tout à l'heure alors qu'il est question de matrices diagonalisables ?

Une solution particulière a été donnée mais à aucun moment, est énoncé très clairement un argument du style: "si une solution existe, voilà comment elle doit être et ça fait d'elle une unique solution" ou bien "les matrices solutions sont forcément comme ceci et il n'y en a pas d'autres"

[Pseuda]

Sauf erreur, A a 2 valeurs propres strictement positives et une strictement négative. On est dans M3(R), donc ... .

[Abilys38]

Il y a trois valeurs propres positives !!

On parle de diagonalisation car ça permet de répondre au problème de manière beaucoup plus simple, sans une multitude de calcul (je pense en tout cas que c'est plus simple). Mais jai mis du temps à comprendre pourquoi ça marchait avec cette méthode !!

Pseuda, pour moi, c'est parce que c'est un sev de dimension 1 et le vecteur propre de A est une base donc l'entendre à lui tout seul. C'est ca que tu me demandais?

[Abilys38]

Trident, il me semble que la commutativité permet d'éliminer tout le reste, non?

[Pseuda]

Il y a trois valeurs propres positives !!

Pseuda, pour moi, c'est parce que c'est un sev de dimension 1 et le vecteur propre de A est une base donc l'entendre à lui tout seul. C'est ca que tu me demandais?

Hum, pourquoi s'embêter à faire des calculs :

http://www.wolframalpha.com/input/?i=%7 ... 1,+1%7D%7D

3 valeurs propres : 1, 3, et -4.

Sinon, c'est pas très clair ta justification. Je te demandais pourquoi les sous-espaces propres de dim 1 de A sont aussi ceux de M. Car ils sont stables par M, l'image par M d'un vecteur propre de A appartient à la même droite vectorielle, donc est proportionnel au vecteur propre, et devient de ce fait-là un vecteur propre de M aussi.

[Elias]

Trident, il me semble que la commutativité permet d'éliminer tout le reste, non?

Oui mais pour en terminer avec l'exercice :

- Déjà, il est vrai que comme le dit Pseuda, A n'a pas 3 valeurs propres positives mais je pense que tu as dû faire une erreur de recopiage quand tu as donné ta matrice (par rapport à ce que fait le corrigé) . Donc je fais comme si A avait des valeurs propres positives toutes distinctes.

- Ensuite, pour mettre les choses dans l'ordre: on cherchait à résoudre l'équation M^2 = A.

Soit M une matrice solution de cette équation.
La matrice A est diagonalisable et on l'a écrit sous la forme A = P D P^(-1) avec D matrice diagonale contenant les valeurs propres de A (positives et distinctes).

Posons ensuite N = P^(-1) M P
On a alors: M = P N P^(-1) et donc comme M^2 = A, il vient: N^2 = D.
Puis là, les arguments de Ben314 prouvent que N est forcément diagonale.

On cherche maintenant l'ensemble des matrices N diagonales vérifiant N^2 = D.
Pour chaque coefficient de la diagonale de D, il y a deux nombres réels dont le carré vaut si et un seul si

Ça doit permettre de trouver toutes les matrices N correspondantes.

Ainsi, on en déduit les candidats M solutions de l'équation.

Reste juste à voir que réciproquement, de telles matrices sont bien solutions de l'équation initiale, ce qui est direct.


Donc en particulier, on peut s'en sortir sans cette histoire de matrices simultanément diagonalisables.

De façon générale, si on prend deux matrices M et A supposées toutes les deux diagonalisables telles que les sous espaces propres de l'une (de l'endomorphime associé) sont stables par l'autre, alors ils sont co diagonalisables (avec la même matrice de passage).
Mais quand on démontre ce résultat,on a besoin que M et A soient diagonalisables.
Or dans cette situation, M n'est pas supposée diagonalisable donc ce théorème que semble utiliser le corrigé ne peut pas s'appliquer.
Ce qui fait marcher le truc en particulier, c'est que les sous espaces propres de A sont de dimension 1 mais ça mérite d'être précisé (cf, message de Pseuda).

Donc du coup, ceci étant précisé, dans ce que j'ai raconté plus haut, au lieu de poser N = P^(1) M P et de dire que N est forcément diagonale etc,on aurait pu dire que M et A sont simultanément diagonalisables donc M s'écrit M = P N P^(-1) avec N diagonale et on terminait de la même façon en cherchant les matrices diagonales N telles que N^2 = D.

Mais moi je conseille de ne pas s'embêter avec cette histoire de matrices simultanément diagonalisables.

[Pseuda]

Parler de matrices simultanément diagonalisables, ou parler de matrices de passage communes via lesquelles les matrices sont diagonales, ou parler de sous-espaces propres communs, tout cela me paraît au final la même chose. Conclusion pour @Abilys : il y a combien de solutions à l'équation M²=A ?

[Abilys38]

Bonsoir à tous !

Pour quand meme clarifier les choses, le corrigé complet présente le calcul des sous espaces propres, etc. Et la petite partie que jai copie n'est que la fin: on avait déjà auparavant diagonalisé A et on savait donc qu'elle était diagonalisable: on déduit ensuite que M l'est forcément aussi.

Sinon, vraiment désolé. En fait, je vous ai donné la matrice A du corrige type, alors que je bosse sur un exo DM tres similaire mais avec une autre matrice.

Voici celle de MON exercice:

5 -2 -2
-2 5 -2
0 -2 5

Donc sauf erreur de ma part, 3 valeurs propres positives., et 8 solutions pour M