Revenons au problème de départ (mais en considérant un entier quelconque
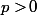
histoire de voir si ça joue ou pas qu'il soit premier).
Si j'ai bien compris,
)
.
Si on écrit la division Euclidienne de
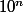
par

:

alors
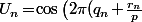\big)\!=\!\cos\big(2\pi\frac{r_n}{p}\big))
qui ne prend qu'un nombre fini de valeurs vu que
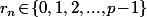
donc la suite est convergente ssi elle est constante à partir d'un certain rang

et, en particulier, on a
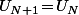
c'est à dire
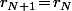
ou bien
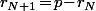
.
Dans le premier cas, on a
p\!=\!10^{N+1}\!-\!10^N\!=\!9.10^N)
donc
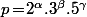
avec
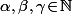
et
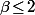
(i.e. 1/p est décimal ou bien admet une écriture décimale périodique à partir d'un certain rang)
Dans le second cas, on a
p\!=\!10^{N+1}\!+\!10^N\!=\!11.10^N)
donc
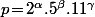
avec
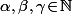
et
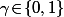
(i.e. 1/p est décimal ou bien admet une écriture décimale style ...545454... ou ...636363... ou ...727272... à partir d'un certain rang)
Et si on se limite à p premier, alors p=2 ou 3 ou 5 ou 11.
