Orde d'un élément dans un groupe

[allmess]

Bonjour,
J'ai une question d'algèbre que j'imagine assez simple mais que je n'arrive pas à résoudre :
combien d'éléments d'ordre 5 y a t'il dans un groupe d'orde 20 ?

Merci d'avance !

[zygomatique]

salut

l'ensemble des éléments d'ordre 5 est un sous-groupes

l'ordre d'un sous-groupe divise l'ordre du groupe

[Ben314]

Salut,

l'ensemble des éléments d'ordre 5 est un sous-groupes

Ca m'étonerais plus que beaucoup vu que tout sous groupe doit contenir le neutre du groupe qui est d'ordre 1 et pas 5.
Sinon, concernant la question, il est tout sauf sûr qu'il y ait une unique réponse vu que des groupes d'ordre 20, il y en a plusieurs.
Sinon, lorsqu'on a des éléments de réponse dans ce type de contexte où on ne connait que le cardinal du groupe et pas le groupe lui même, c'est souvent en utilisant les Théorèmes de Sylow.

[allmess]

Merci pour vos réponses !
En me basant sur le 3e théorème de Sylow, on aurait , soit donc 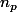le nombre cherché ; on a et , d'où ?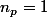
Merci encore d'avance !

[zygomatique]

bien sur avec le cas particulier de l'élément neutre ...