Help me !!!!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 10 Mar 2017, 14:28
par mouloud » 10 Mar 2017, 14:28
j ai pas vraiment compris l exercice suivant
ci joint une photo de le exercice

- Fichiers joints
-

- dl exo.png (48.4 Kio) Vu 546 fois
-
aviateur
 par aviateur » 10 Mar 2017, 14:55
par aviateur » 10 Mar 2017, 14:55
Bonjour
commence par donner le domaine de définition et puis on verra.
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 10 Mar 2017, 15:09
par mouloud » 10 Mar 2017, 15:09
1/le domaine de definition:
Df=]-1,1[
2/la demonstration:
/\sqrt{1-x^2} \Leftrightarrow y*\sqrt{1-x^2}=arcsin(x))
*par derivation on a :
'=1\div \sqrt{1-x^2})
en multiplient par
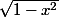
on trouvent :
-xy=1)
------------------------------------------(*)
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 10 Mar 2017, 16:05
par mouloud » 10 Mar 2017, 16:05
3/en appliquent la formule de leibniz sue l equantion (*) on trouve :
-x.y \right]^n =0)
^(^n^)=\sum_{k=0}^{n}{x^(k^).y^(n-k^)}=x.y^(n^)+n.y^(n-1^))
------------(1)
et on a :
 \right]^n = (1-x^2)y^n^+^1-2nxy^n -(n^2-n)y^n-^1)
------------(2)
(1)-(2):
- Fichiers joints
-

- dl1png.png (3.45 Kio) Vu 532 fois
-
aviateur
 par aviateur » 10 Mar 2017, 17:14
par aviateur » 10 Mar 2017, 17:14
Je ne comprends pas ta formule de Leibniz qui devrait faire intervenir les coefficients C_n^k
dans ta somme.
Néanmoins les résultats sont bons.
La question 4 est facile: il suffit de remplacer x par 0 dans la formule obtenue à la question 3.. On a ainsi une relation de récurrence entre les dérivées de même parité en (0). Et ainsi on doit en déduire y^{2n} (0) .
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 10 Mar 2017, 17:54
par mouloud » 10 Mar 2017, 17:54
merci bcp

j espere que tu me guideras jusqu a la fin
4/que vaut
 ?)
pour x=0 on a:
une relation de récurrence entre les dérivées de même parité en (0)

-----------------
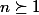
si : n+1 = 2p alors :
=(2p-1)y^{2(p-1)} :p\geq 1)
et tant que
=arcsin(0)/\sqrt{1-0^2}=0)
=0 :p\geq 1)
5/suivant la 4eme question :
ou remplace 2p par 2n+1 on aura le résultats
- Fichiers joints
-
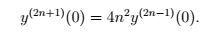
- dl1png.png (2.27 Kio) Vu 513 fois
-
aviateur
 par aviateur » 10 Mar 2017, 18:11
par aviateur » 10 Mar 2017, 18:11
oui c'est exactement cela
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 10 Mar 2017, 18:15
par mouloud » 10 Mar 2017, 18:15
la 6 eme question et aussi simple en a qu a écrire le dl en (0) et en utilisent le 2 question précédentes
=0)
=4n^2.y^{2p-1}(0))
-
aviateur
 par aviateur » 10 Mar 2017, 18:18
par aviateur » 10 Mar 2017, 18:18
Oui la fonction est de classe C infini sur son domaine de définition. Donc elle admet un DL en 0 à tout ordre et il est donné par son développement de Taylor que l'on obtient grâce au calcul des dérivées en 0.
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 10 Mar 2017, 19:13
par mouloud » 10 Mar 2017, 19:13
un dernier coup de main stp

apres avoir fait cela :
=arcsin^2(x)=(1-x^2).f^2(x))
le développement de
=\left[x+3/2x^3+8/15x^5+....+[4^n*(n^2!)]/(2n+1)! \right]^2)
ms a l ordre n pas 2n+1
-
aviateur
 par aviateur » 10 Mar 2017, 23:21
par aviateur » 10 Mar 2017, 23:21
Non....
Tout simplement tu calcul la dérivée de arcsin(x)^2 et tu vas tomber à un facteur près sur f(x).
Ce qui va donner directment le résultat.
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 11 Mar 2017, 00:02
par mouloud » 11 Mar 2017, 00:02
dacc , ms peut tu m explique pour quoi calculer la d arcsin2(x)/dx
-
mouloud
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Mar 2017, 14:20
-
 par mouloud » 11 Mar 2017, 13:17
par mouloud » 11 Mar 2017, 13:17
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités

