[/Voila je n'arriva pas à rediger correctement cette exo
merci de me montrer une redaction correcte.
Fonction Bijective, EXO Help
4 messages
- Page 1 sur 1
Fonction Bijective, EXO Help
par cybero » 11 Nov 2007, 14:19
[/Voila je n'arriva pas à rediger correctement cette exo
merci de me montrer une redaction correcte.
par Nightmare » 11 Nov 2007, 14:31
Bonjour :happy3:
Un conseil pour le premier, fait un tableau de tes résultats, on voit très bien comment les nombres se générent.
Un conseil pour le premier, fait un tableau de tes résultats, on voit très bien comment les nombres se générent.
par Nightmare » 11 Nov 2007, 14:41
Bref,
pour l'injectivité c'est simple.
La surjectivité :
Soit N naturel fixé.
Il existe un n tel que}{2}<N<\frac{(n+1)(n+2)}{2})
On pose}{2})
On a(n+2)}{2}-\frac{n(n+1)}{2})
ie 
donc 
Et=\frac{n(n+1)}{2}+N-\frac{n(n+1)}{2}=N)
donc f est surjective.
pour l'injectivité c'est simple.
La surjectivité :
Soit N naturel fixé.
Il existe un n tel que
On pose
On a
Et
donc f est surjective.
par aviateurpilot » 11 Nov 2007, 14:52
on a }{2},\frac{(n+1)(n+2)}{2}-1|])
(reunion de parties disjointes)
donc}{2}\le y\le \frac{(n+2)(n+1)}{2}-1)
et on prend }{2})
on a bien)
unique dans 
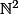
et (n+2)-n(n+1)}{2}-1=n)
donc
est bijective.
)
n'a pas de limite
car}{2}}\to 0)
et }{2}+n}\to +\infty)
donc
on a bien
donc
car
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :