Calcule Conbinatoire
Olympiades mathématiques, énigmes et défis
-
washwash
- Membre Naturel
- Messages: 63
- Enregistré le: 19 Déc 2016, 13:36
-
 par washwash » 21 Déc 2016, 09:06
par washwash » 21 Déc 2016, 09:06
Bonjour
Je cherche à calculer la formule suivante:
^{\displaystyle\sum_{j \in T\cup S} z_j}\sum_{A \subseteq \overline{z_T}\cup S\setminus \overline{z_{S_2}}}\frac{3^{|T\setminus \overline{z_T}|}(2)^{|A \cap \overline{z_T}|}2^{|A \cap (S_1\setminus \overline{z_{S_1}})|}}{n+|\overline{z_T}|-|T|-|A|})
avec,
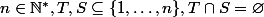
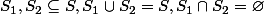
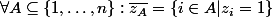
-
washwash
- Membre Naturel
- Messages: 63
- Enregistré le: 19 Déc 2016, 13:36
-
 par washwash » 22 Déc 2016, 09:00
par washwash » 22 Déc 2016, 09:00
Une autre façon à écrire la formule :
^{|B|+|C|+|D|}\sum_{A \subseteq B \cup (S \setminus D)}\frac{3^{|T\setminus B|}(2)^{|A \cap B|}2^{|A \cap (S_1\setminus C)|}}{n+|B|-|T|-|A|})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités