Bonjour,
je souhaiterais m'inscrire à un concours de maths pour 1re S.
J'ai trouvé un QCM bilan sur internet mais il n'y a pas de corrigé... Il faut impérativement que je regardes si j'ai bien assimilé le cours. Voici les liens du QCM : .
Pouvez vous me fournir un corrigé svp ? j'ai tout fait jusqu'au 21.. sauf que je ne suis pas sûr pour la 8
QCM bilan
11 messages
- Page 1 sur 1
Salut,
Pour une bonne partie des question concernant cette fonction f (donc 18 à 26), il te suffit de dresser proprement le tableau de variation et de "lire" les réponses dans le tableau des variations de f.
Tu as vu les dérivées ?
Tu as calculé la dérivée de la fonction f ? étudié le signe de cette dérivée ?
Pour une bonne partie des question concernant cette fonction f (donc 18 à 26), il te suffit de dresser proprement le tableau de variation et de "lire" les réponses dans le tableau des variations de f.
Tu as vu les dérivées ?
Tu as calculé la dérivée de la fonction f ? étudié le signe de cette dérivée ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si =-x^3+3x+15) alors f est définie, continue, dérivable sur R tout entier et, pour tout réel x, on a
alors f est définie, continue, dérivable sur R tout entier et, pour tout réel x, on a
=-3x^2+3=-3(x^2-1)=-3(x-1)(x+1)) qui est =0 en x=-1 et x=1 ; >0 si x est dans ]-1,1[ et +oo lorsque x->-oo, décroit jusqu'à f(-1)=13 puis croit jusqu'à f(1)=17 puis décroit et f(x)->-oo lorsque x->+oo (à mettre dans un tableau, c'est plus facile à lire)
qui est =0 en x=-1 et x=1 ; >0 si x est dans ]-1,1[ et +oo lorsque x->-oo, décroit jusqu'à f(-1)=13 puis croit jusqu'à f(1)=17 puis décroit et f(x)->-oo lorsque x->+oo (à mettre dans un tableau, c'est plus facile à lire)
On a donc :
Q18) => (a) : c.f. ci dessus
Q19) => (c) : (f(h)-15)/h = (f(h)-f(0))/(h-0) tend vers f'(0)=3 lorsque x->0
Q20) => (c) : Si f est dérivable en xo, la tangente en (xo,f(xo)) est y-f(xo)=f'(xo)(x-xo)
Q21) => (b) : c.f. ci dessus
Q22) => (a) VRAI : 3-3x²=4 n'a pas de solution ; (c) VRAI : 3-3x²=0 a une seule solution (x=0) ; (d) VRAI : 3-3x² s'annule 2 fois (en x=-1 et en x=1)
Q23) => (b) + (c) : c.f. ci dessus
Q24) => Vu les variations, il existe un unique xo dans ]1,+oo[ telle que f(xo)=0 et f est >0 sur ]-oo,xo[ et (a) VRAI : Vu les variations, 17=f(1) est bien un maximum local, c'est par exemple le maximum pour x dans [-1,2] où la fonction croit puis décroit, mais ce n'est pas un maximum global vu que la fonction tend vers +oo lorsque x->-oo.
 (c) VRAI : f admet (évidement) un maximum sur [-2,0]. Comme elle est décroissante puis croissante sur [-2,0] son maximum est le plus grand des deux nombres f(-2)=17 et f(0)=15. C'est donc f(-2)=17 (qui n'a rien à voir avec le maximum local en x=1).
(c) VRAI : f admet (évidement) un maximum sur [-2,0]. Comme elle est décroissante puis croissante sur [-2,0] son maximum est le plus grand des deux nombres f(-2)=17 et f(0)=15. C'est donc f(-2)=17 (qui n'a rien à voir avec le maximum local en x=1).
Q26) => (a) VRAI : Vu les variations, 13=f(-1) est bien un minimum local, c'est par exemple le minimum pour x dans [-2,1] où la fonction décroit puis croit, mais ce n'est pas un minimum global vu que la fonction tend vers -oo lorsque x->+oo.
 (c) VRAI : On vient de voir que 13=f(-1) est le minimum de f sur [-2,1] mais le problème, c'est qu'ensuite sur [1,2] la fonction décroit donc risque de passer en dessous de ce minimum. Sauf qu'en fait f(2)=13 donc f(x)>=13 pour x dans [1,2] (car f est décroissante sur cet intervalle) donc 13 est bien le minimum de f sur [-2,2] (par contre, ça ne serait plus le minimum sue [-2,2.1] vu qu'on aurait f(2.1)<13)
(c) VRAI : On vient de voir que 13=f(-1) est le minimum de f sur [-2,1] mais le problème, c'est qu'ensuite sur [1,2] la fonction décroit donc risque de passer en dessous de ce minimum. Sauf qu'en fait f(2)=13 donc f(x)>=13 pour x dans [1,2] (car f est décroissante sur cet intervalle) donc 13 est bien le minimum de f sur [-2,2] (par contre, ça ne serait plus le minimum sue [-2,2.1] vu qu'on aurait f(2.1)<13)
On a donc :
Q18) => (a) : c.f. ci dessus
Q19) => (c) : (f(h)-15)/h = (f(h)-f(0))/(h-0) tend vers f'(0)=3 lorsque x->0
Q20) => (c) : Si f est dérivable en xo, la tangente en (xo,f(xo)) est y-f(xo)=f'(xo)(x-xo)
Q21) => (b) : c.f. ci dessus
Q22) => (a) VRAI : 3-3x²=4 n'a pas de solution ; (c) VRAI : 3-3x²=0 a une seule solution (x=0) ; (d) VRAI : 3-3x² s'annule 2 fois (en x=-1 et en x=1)
Q23) => (b) + (c) : c.f. ci dessus
Q24) => Vu les variations, il existe un unique xo dans ]1,+oo[ telle que f(xo)=0 et f est >0 sur ]-oo,xo[ et (a) VRAI : Vu les variations, 17=f(1) est bien un maximum local, c'est par exemple le maximum pour x dans [-1,2] où la fonction croit puis décroit, mais ce n'est pas un maximum global vu que la fonction tend vers +oo lorsque x->-oo.
Q26) => (a) VRAI : Vu les variations, 13=f(-1) est bien un minimum local, c'est par exemple le minimum pour x dans [-2,1] où la fonction décroit puis croit, mais ce n'est pas un minimum global vu que la fonction tend vers -oo lorsque x->+oo.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Comme la fonction 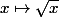 est croisante sur son domaine de définition, la monotonie de ta fonction f sur son domaine de définition est la même que celle de
est croisante sur son domaine de définition, la monotonie de ta fonction f sur son domaine de définition est la même que celle de =-2x^2+6) dont la dérivée est donnée par
dont la dérivée est donnée par =-4x) .
.
Donc f est croissante sur puis décroissante sur
puis décroissante sur  : (a) et (b) VRAIS
: (a) et (b) VRAIS
Donc f est croissante sur
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
