Division Polynomiale

[glouglu]

Bonjour ,

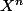
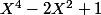
Je cherche le reste de par pour tout n.

Le polynome a 2 racines (-1 et 1) et le reste s'écrit comme un polynome de degré 3, j'ai seulement 2 équations.

Comment puis-je faire ? :hein:

[deltab]

Bonsoir.

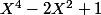
N'oublies que admet 4 racines dans et voilà tes 4 équations.

[glouglu]

Bonsoir.

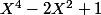
N'oublies que admet 4 racines dans et voilà tes 4 équations.

yhbvreibfuirepbfierpmbfeipm

[Faraziel]

Bonjour,

Reprend ta factorisation, elle est fausse.

Par ailleurs je pense que c'est plus une étourderie que autre choses.

[mathelot]

bonsoir,

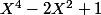
comme est un carré, p-e travailler également avec la dérivée,

[glouglu]

Bonjour,

Reprend ta factorisation, elle est fausse.

Par ailleurs je pense que c'est plus une étourderie que autre choses.

L'énoncé me donne . Xcas me donne le meme dévéloppement que le mien ....

[Faraziel]

Ouais pardon, je suis à la pèche, la factorisation est bonne...
Mille excuse, c'est juste la forme de la mienne qui était différente.
J'était arrivé à (x²-1)², ce qui est exactement la même chose.

Mea Culpa

[chan79]

Ouais pardon, je suis à la pèche, la factorisation est bonne...
Mille excuse, c'est juste la forme de la mienne qui était différente.
J'était arrivé à (x²-1)², ce qui est exactement la même chose.

Mea Culpa

Salut
Envisager deux cas selon la parité de n et utiliser la dérivée comme indiqué par mathelot

[OY9151]

Bonjour tout le monde ,

pour la problème posé la réponse peut être obtenue facilement par synthètisation de la division euclidienne exécutée par la méthode d'O.R. et ce en écrivant x^n sous la forme
x^n = x^n + 0x^(n-1) + 0x^(n-2)+....+ 0x^5 + 0x^4 + 0x^3 + 0x^2 + 0x+0

Salut .

[Ben314]

Bonjour tout le monde ,

pour la problème posé la réponse peut être obtenue facilement par synthètisation de la division euclidienne exécutée par la méthode d'O.R. et ce en écrivant x^n sous la forme
x^n = x^n + 0x^(n-1) + 0x^(n-2)+....+ 0x^5 + 0x^4 + 0x^3 + 0x^2 + 0x+0

Salut .

Pourquoi faire simple quand on peut faire compliqué...

[OY9151]

Bonjour ,

" Pourquoi faire simple quand on peut faire compliqué... :"

vous avez parfaitement raison M. Ben314 (en inversant bien sur dans cette phrase la position des mots....) et par conséquent chacun (en premier M. GLOUGLU) se doit de rejeter les termes de ma solution qui (peut être!?) n'aura d’intérêt que si on demandait en plus l'expression du quotient Q(x) en fonction de n.
Salutations.