Ce forum ayant finalement posé beaucoup de questions, je me permets de faire un petit topo:
Tout d'abord on définit
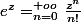
; cette série étant absolument convergente, tout est permis, en particulier:
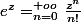
;
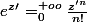
donc
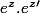
=
}{k!.(n-k)!})
; et comme
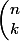
=
!)
, on obtient
}{n!})
=
^n}{n!})
=
)
. désolé pour l'écriture, mais je ne me ferais jamais aux bornes latex!
Cette propriété fondamentale étant établie, tout est possible, à commencer par l'exponentielle réelle; on a tout, les propriètes, la dérivée (

)'=

,
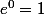
,
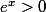
si
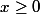
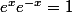
d'où
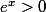
; on a tout pour définir ln(x) avec toutes ses propriétés (limites incluses); l'unicité de

se montre comme on veut; bref, on évite toutes les difficultés.
Ensuite, on passe au cosinus et au sinus sans aucun problème: en restant dans le cadre réel, on a cos(x) = Re(
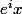
) et sin(x)=Im(
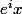
), ce qui donne les formules d'Euler et permet de trouver absolument toutes les formules trigonométriques; dans la foulée, on définit sin(z) et cos(z) (on s'éloigne beaucoup du cercle trigo!). Reste à définir

. Si on considére la série entière qui définie cos(x), la valeur absolue de ses termes n'est pas toujours décroissante, mais est unimodale et une fois le terme modal dépassé, on peut appliquer le critère des séries alternées qui exprime que la valeur absolue du reste est majorée par la valeur absolue du 1°terme négligé.
Ainsi sur [0; 2], pour la fonction cos le terme modal est éventuellement
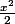
donc, on a cos(0)=1 et cos(2)
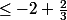
0 de cos(x).
Une fois

défini, tout le reste vient.
Et notre bon vieux cercle trigo? Il est définit par
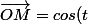\vec{i}+sin(t)\vec{j})
mais rien n'oblige à prendre le repère physiquement orthonormé!
C'est là que s'achève cette belle démarche, car la notion d'angle est totalement exclue et il va bien falloir pour des raisons pédagogiques évidentes que
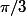
corresponde à 60°!
A titre anecdotique, je signale qu'au moment de la mise en place du programme des mathématiques modernes, bon nombre d'inspecteurs généraux étaient contre l'introduction du mot"angle" dans le programme; finalement, on a eu droit à l'angle d'une rotation vectorielle!
Autre anecdote, quand j'étais tout jeune prof, j'avais un collègue au demeurant très sympathique, qui donnait un exercice de géométrie où il y avait 5 ou 6 parallélogrammes à déterminer, mais qui employait la notation

et qui concluait son corrigé par: "un dessin de la figure ne s'imposant pas, je ne le ferais pas"
Conclusion: ce n'est pas parce qu'une démarche est jolie, qu'elle est pédagogiquement intéressante !
