Inégalité de Taylor-Lagrange

[Romanouch]

Bonjour,

Dans l'énoncé de l'inégalité de Taylor-Lagrange, je trouve à chaque fois l'utilisation du terme "sup de f dérivée n+1 ième" (je ne rentre pas dans le détail de l'inégalité, ce n'est pas le sujet ici).

Je ne comprends pas pourquoi on ne parle pas du max, puisqu'il existe et que donc le sup = le max.

Si on veut démontrer l'inégalité, on va utiliser le théorème des bornes atteintes, pour dire que la fonction est bornées sur l'intervalle en question.
Vu que le théorème dit: "et atteint ses bornes", on sait que la valeur est un max, alors pourquoi parler de sup?

Est-ce seulement "comme ça" ou y-a-il une raison mathématique qui m'échappe?
Merci d'avance.

[zygomatique]

salut

parce que l'important c'est que ça soit borné donc un sup suffit ...

[L.A.]

Bonjour.

Non, pour moi il n'y a aucune raison d'écrire sup à la place de max si c'est un max. Mais peut-être qu'on préfère écrire sup dans un contexte continu et max dans un contexte discret, même si c'est moins précis et éventuellement plus troublant. Il faut faire un peu attention et ne pas s'alarmer...

[Romanouch]

Bonjour,

Merci de vos réponses rapides. C'est quand même étonnant, si x est inférieur à 3, on peut écrire que x est inférieur à 1000, mais bon, c'est moins précis. Ça contient moins d'information.
Ici, le sup et le max sont confondus, donc ce n'est pas "moins précis", mais dans le principe c'est surprenant. Il y a peut être une raison, qui sait.

[adrien69]

Bah la raison principale ici c'est que l'inégalité est vraie sur tout intervalle, même ouvert, et pour le coup, s'il est ouvert ton sup n'est pas nécessairement un max.

Et puis le théorème de Weierstrass (ton truc des bornes atteintes, d'ailleurs c'est quoi ce nom bizarre ??) c'est un peu la base de l'analyse. On suppose que les gens savent s'en servir sans ciller.

Ensuite le sup c'est LE PLUS PETIT des majorants. Donc écrire sup au lieu d'écrire max, ce n'est pas du tout écrire x0 au lieu de .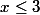

Sans oublier que le théorème marche aussi si ta dérivée nième est continue par morceaux. Là tu as encore moins sup=max.

Ce qui veut aussi dire que le théorème peut ne rien t'apprendre : tu te retrouveras à montrer qu'une quantité est inférieure ou égale à l'infini. Et donc il faudra utiliser d'autres outils.

[Romanouch]

Salut,

Merci pour ta réponse.

Je ne savais pas qu'on appelait le théorèmes des bornes atteintes, théorème de Weierstrass, tu me l'apprends. Je te confirme quand même qu'on l'appelle aussi théorème des bornes atteintes.

Par contre, ce théorème s'applique sur un segment, et je ne trouve pas de référence aux intervalles ouverts ou aux fonctions CM, est-ce que tu aurais un lien vers des explications?
Même chose pour la majoration par l'infini, je n'ai pas bien compris ce que tu voulais dire.

[adrien69]

Par contre, ce théorème s'applique sur un segment, et je ne trouve pas de référence aux intervalles ouverts ou aux fonctions CM, est-ce que tu aurais un lien vers des explications?

Je ne parle pas du "théorème des bornes atteintes" hein ! C'est l'inégalité de Taylor-Lagrange qui s'applique sur tout type d'intervalle.

Je n'ai pas de lien mais c'est franchement évident dès qu'on réfléchit à ce qu'on fait. Le théorème de Taylor Lagrange te dit que dès que tu as une fonction n+1 fois dérivable sur un intervalle I (avec la (n+1)ème dérivée intégrable, par exemple, continue par morceaux) et que tu peux majorer la (n+1)eme dérivée en valeur absolue par un certain M sur I, alors ton reste sera plus petit, en valeur absolue que M*blabla avec le point de calcul du développement qui est dans I et la variable aussi.

En particulier, M=sup(|f^(n+1)|) sur I marche toujours, même s'il est infini. Mais dans ce cas-là ça ne t'apprend rien parce que tu diras que ton reste est inférieur ou égal à l'infini, ce qui est vrai pour tout nombre... Et en plus, l'infini ne sera pas atteint sur I puisque f^(n+1) est définie sur I.


Bref, je résume : sup et pas max, parce que sup pas toujours atteint et parce qu'on n'est pas idiots et qu'on sait remplacer le sup par le max QUAND ON EN A LE DROIT. Et la borne que tu obtiens en utilisant le sup a le droit d'être infinie. Mais elle ne te sert alors à rien.

[Romanouch]

Oui, je comprends bien tout cela, mais je persiste, l'existence de ce fameux sup vient du fait qu'on se place sur un segment (Th Weierstrass).

Si j'appelle le point de calcul du développement: a, et la variable x, l'existence d'un max viendra de la continuité de la dérivée (n+1) ième sur [a;x] ou [x;a].
Donc, même si l'inégalité s'applique sur un intervalle ouvert, en chaque point de l'intervalle, le sup est un max.

Non?

[adrien69]

Si j'appelle le point de calcul du développement: a, et la variable x, l'existence d'un max viendra de la continuité de la dérivée (n+1) ième sur [a;x] ou [x;a].

Et tu fais quoi si elle est continue PAR MORCEAUX ?

[adrien69]

Mais sinon oui, sup=max car continue et segment [a,x]
Et comme ça fait moins d'une ligne à écrire, tu comprendras pourquoi on met sup et pas max. Parce que ça ne sert à rien de gagner trois mots, et que c'est dangereux voire parfois faux si on n'a pas le résultat de continuité.

[Romanouch]

Je suis désolé, mais l'énoncé de l'inégalité de Taylor-Lagrange est très clair sur le sujet: on considère une fonction C n+1 sur un intervalle, donc de dérivée (n+1)ième continue sur un intervalle.

Si la fonction dérivée n+1 ième n'est pas continue, je ne vois même pas pourquoi tu parles de sup, puisqu'il n'existe pas forcément, là vraiment je ne saisis pas...

Dans le cas de la formule de Taylor (c'est le sujet de cette discussion), le terme max me semble correct, et ma question initiale toujours non résolue.

[adrien69]

Je suis désolé, mais l'énoncé de l'inégalité de Taylor-Lagrange est très clair sur le sujet: on considère une fonction C n+1 sur un intervalle, donc de dérivée (n+1)ième continue sur un intervalle.

TON énoncé est très clair à ce sujet. Et ce n'est clairement pas le plus général. Ton cas n'est qu'un corollaire, ce que tu remarqueras si tu en lis la preuve.

Le sup existe toujours. C'est parfois l'infini, parfois un truc fini. Mais il existe toujours. Par convention.

Maintenant, montre-moi l'endroit où tu as précisé que ta dérivée (n+1)ème devait être continue avant ton dernier message ?

Donc admettons maintenant que tu veuilles ton énoncé avec la continuité et c'est tout (ce que je trouve diablement stupide mais passons), on écrit sup plutôt que max pour la simple et bonne raison que tout le monde est capable de le changer en max soi-même.

[Romanouch]

Non, ce n'est pas "diablement stupide", si tu ouvres un livre de maths, tu risques de trouver PARTOUT cet énoncé de l'inégalité de Taylor-Lagrange.

Maintenant, je veux bien que tu me donnes le lien vers le cas plus général de l'inégalité de Taylor-Lagrange dont tu parles, c'est le but de ma question initiale après tout.
En attendant, tes "c'est évident", "tellement simple", "si on n'est pas idiots" ou "tu remarqueras" ne sont ni constructifs, ni rigoureux d'ailleurs.

Le sup n'existe pas toujours, l'ensemble R par exemple ne possède pas de borne sup, et la convention appelant borne supérieure l'infini n'existe pas. On est en France, tu es libre d'en créer une perso si ça t'aide, tu fais ce que tu veux en fait ;)

[adrien69]

Je pensais que c'était une discussion informelle, pas rigoureuse (tout le monde s'y est laissé prendre d'ailleurs). Admettons encore une fois (sinon, tu es en MPSI ou un truc du genre non ?).

Bon premier lien : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Taylor#In.C3.A9galit.C3.A9_de_Taylor-Lagrange

Tu remarqueras que nulle part on n'a supposé la continuité de f^(n+1).

http://www-fourier.ujf-grenoble.fr/~rombaldi/AgregInterne/Oral1/218.pdf

Idem.

http://www.math.u-psud.fr/~perrin/CAPES/analyse/fonctions/formulesdetaylor(07).pdf

Dans celui-là il n'est pas fait mention de l'inégalité, mais tu remarqueras que le départ est le même que le papier précédent.


Mais je pense que tu as dû démontrer l'inégalité de Taylor-Lagrange à partir de la formule avec reste intégral. Alors que justement pour avoir une version plus costaude du théorème, il faut partir de la formule dite égalité de Taylor-Lagrange (celui qui est une généralisation des accroissements finis), et qui est hors-programme en MPSI.

Et puis concernant les bouquins, n'oublie pas que ce sont des bouquins pédagogiques que tu utilises, ils n'ont aucune prétention à l'exhaustivité.


Pour information, ton inégalité tiendrait même si la dérivée (n+1)ème de ta fonction était la fonction caractéristique de , c'est dire...

Pour ce qui est de l'infini comme borne sup peut-être qu'à un niveau élémentaire ce n'est pas une convention. Dans ce cas-là je m'excuse, c'est juste que dans les théories moins élémentaires de l'intégration que celle de Riemann on considère plus facilement la droite réelle achevée (avec les deux infinis, ce qui nous donne donc parfois l'infini comme borne sup') que la droite réelle tout court.

[Romanouch]

Je pensais que c'était une discussion informelle, pas rigoureuse (tout le monde s'y est laissé prendre d'ailleurs). Admettons encore une fois (sinon, tu es en MPSI ou un truc du genre non ?).

Oui, j'essaie d'être rigoureux, sinon je ne comprends rien.
Non, je ne suis pas en MPSI, je suis ingénieur, passé par les classes prépa il y a 10 ans, et parfois je me pose de drôles de questions

Bon premier lien : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Taylor#In.C3.A9galit.C3.A9_de_Taylor-Lagrange
Tu remarqueras que nulle part on n'a supposé la continuité de f^(n+1).
http://www-fourier.ujf-grenoble.fr/~rombaldi/AgregInterne/Oral1/218.pdf
Idem.
http://www.math.u-psud.fr/~perrin/CAPES/analyse/fonctions/formulesdetaylor(07).pdf
Dans celui-là il n'est pas fait mention de l'inégalité, mais tu remarqueras que le départ est le même que le papier précédent.

Oui, bien sûr que l'hypothèse de continuité de f dérivée (n+1)ième n'est pas nécessaire quand on fait l'hypothèse qu'elle est majorée!!!
Moi je pars de la continuité sur un segment pour déduire qu'elle est majorée, nous ne partons pas des mêmes hypothèses.

Pour essayer de résumer, toi tu pars de l'existence d'un majorant et tu en déduis l'inégalité (pas besoin de continuité).
Moi je pars de la continuité de la dérivée et j'en déduis l'existence d'un maximum.
Dans ton cas, prendre le sup est logique, dans le mien, prendre le max le serait sans doute plus.

Dans tous les énoncés que je trouve de l'inégalité avec condition de continuité de la dérivée (n+1), le terme employé est sup... Est-ce pour uniformiser? Avec le sup, l'inégalité reste vraie dans un cas comme dans l'autre? Qu'en penses-tu?

[adrien69]

Dans tous les énoncés que je trouve de l'inégalité avec condition de continuité de la dérivée (n+1), le terme employé est sup... Est-ce pour uniformiser? Avec le sup, l'inégalité reste vraie dans un cas comme dans l'autre? Qu'en penses-tu?

Je suis presque certain que c'est pour ça.
Et aussi parce que ta version est un corollaire immédiat (via les "bornes atteintes") de la version que j'en donne. Donc les mecs qui rédigent leur bouquin ne s'embêtent généralement pas à enlever le sup (ils copient-collent trèèèèès sûrement la formule quelque part, parce que bon, LaTeX c'est cool, les formules à rallonge aussi, mais les deux ensemble, c'est vraiment insupportable).

[Romanouch]

Je suis presque certain que c'est pour ça.
Et aussi parce que ta version est un corollaire immédiat (via les "bornes atteintes") de la version que j'en donne. Donc les mecs qui rédigent leur bouquin ne s'embêtent généralement pas à enlever le sup (ils copient-collent trèèèèès sûrement la formule quelque part, parce que bon, LaTeX c'est cool, les formules à rallonge aussi, mais les deux ensemble, c'est vraiment insupportable).

Merci pour cette discussion.
Au plaisir de te lire lors d'un prochain échange, c'est sympa de rencontrer quelqu'un qui aime vraiment ce domaine.
Salut.