Bonjour, exercice sur les produits scalaires
14 messages
- Page 1 sur 1
bonjour, exercice sur les produits scalaires
pouvez-vous m'aidé a comprendre cet exercice tout en m'expliquant s'il-vous plait car j'ai un devoirs de maths très bientôt et je refais des exercices pour m'aider a comprendre cet leçon.
Voici mon exercice :
IJK est un triangle avec IJ=16, IK=10 et KJ=12.
a/Déterminer les mesures de ses tris angles (à10^-1 près en degrés).
b/ En deduire la valeur exacte de IJ.IK, ainsi que la longeur de la hauteur issue de K.
IJ.IK (=produit scalaire)
Merci de votre aide
Voici mon exercice :
IJK est un triangle avec IJ=16, IK=10 et KJ=12.
a/Déterminer les mesures de ses tris angles (à10^-1 près en degrés).
b/ En deduire la valeur exacte de IJ.IK, ainsi que la longeur de la hauteur issue de K.
IJ.IK (=produit scalaire)
Merci de votre aide
scientifique21 a écrit:pouvez-vous m'aidé a comprendre cet exercice tout en m'expliquant s'il-vous plait car j'ai un devoirs de maths très bientôt et je refais des exercices pour m'aider a comprendre cet leçon.
Voici mon exercice :
IJK est un triangle avec IJ=16, IK=10 et KJ=12.
a/Déterminer les mesures de ses tris angles (à10^-1 près en degrés).
b/ En deduire la valeur exacte de IJ.IK, ainsi que la longeur de la hauteur issue de K.
IJ.IK (=produit scalaire)
Merci de votre aide
Salut,
Est-ce que tu connais la loi des sinus ?
paquito a écrit:Théorème d'Al Kashi: dans tout triangle ABC, BC²=AB²+AC²-2.ABxACxcos(BAC). Donc
cos(BAC)=(AB²+AC²-BC)/(2.ABxAC). Tu as aussi AB.AC=1/2(AB²+AC²-BC²).
En plus tu as aire de (ABC)=1/2 AHxBC =1/2ABxACXsin(BAC), Donc AH=(2xaire(ABC))/BC.
Adapte ces résultats de cours à IJK.
Cmment dois-je proceder pour les remplacer car je ne comprend pas trop cet leçon ....
scientifique21 a écrit:Cmment dois-je proceder pour les remplacer car je ne comprend pas trop cet leçon ....
----------------------------
scientifique21,
Je vais t'aider à trouver le 1er des trois angles du triangle IJK :
D'après ce que t'on dit nos collègues précédemment avec Al-Kashi, je pense que tu peux écrire que k² = i² + j² -2ij cos K
D'où si tu isole cos K, ça donne :
cos K =
et tu nous dit que l'angle K est égal à combien de degrés à 10^-1 degré prés ?.....
QUE TU PEUX VERIFIER, avant de nous l'écrire, AVEC TON RAPPORTEUR SUR TA FIGURE !....
indice : sur ma figure je trouve un peu plus que l'angle droit, mais dis-nous combien exactement (à 10^-1 près comme demandé dans l'énoncé) !....
Ijk
scientifique21 a écrit:Cmment dois-je proceder pour les remplacer car je ne comprend pas trop cet leçon ....
----------------------------
scientifique21,
Je vais t'aider à trouver le 1er des trois angles du triangle IJK :
D'après ce que t'on dit nos collègues précédemment avec Al-Kashi, je pense que tu peux écrire que k² = i² + j² -ij cos K
D'où si tu isole cos K, ça donne :
cos K =\frac{i²+j²-k²}{2ij}
et tu nous dit que l'angle K est égal à combien de degrés à 10^-1 degré pré ? QUE TU PEUX VERIFIER avant AVEC TON RAPPORTEUR SUR TA FIGURE !....
laetidom a écrit:----------------------------
scientifique21,
Je vais t'aider à trouver le 1er des trois angles du triangle IJK :
D'après ce que t'on dit nos collègues précédemment avec Al-Kashi, je pense que tu peux écrire que k² = i² + j² -ij cos K
D'où si tu isole cos K, ça donne :
cos K =
et tu nous dit que l'angle K est égal à combien de degrés à 10^-1 degré pré ? QUE TU PEUX VERIFIER avant AVEC TON RAPPORTEUR SUR TA FIGURE !....
Bonjour
Il manque un petit 2 dans la formule d'Al Kashi
scientifique21,
Comme tu m'a dis que tu souhaitais absolument comprendre le produit scalaire (PS), et que tu ne semble pas bien maitriser l'outil (vu que tu commence !), je vais te donner quelques éléments :
b) toujours pareil, disposer devant soi d'une figure que tu construit la plus "précise et complète" possible (en fonction des données du sujet), c'est la base !, et savoir son cours :
-------------------------------------------------------------------
le PS de 2 vecteurs est :
1 ) le produit des modules des 2 vecteurs par le cosinus de l'angle entre les vecteurs,
ou bien :
2) simplement le produit du module de l'un des vecteurs par le module du projeté orthogonal (sur la droite support du 1er vecteur) du second vecteur ! (reprendre le cours pour bien cerner visuellement la chose !!!)
------------------------------------------------------------------
Donc IJ.IK (le . veut dire Produit scalaire) =
avec 1)
IJ.IK = IJ x IK x cos I = 16 x 10 x (53/80) = 106
(dans le a) tu auras calculé le cos I, entre autres)
(le x veut dire multiplié)
avec 2)
IJ.IK =106=IJ x IH
(H étant le projeté orthogonal de K sur IJ)
D'où IH = 106/16
puis avec Pythagore tu trouve la valeur de HK qui est la longueur de la hauteur issue de K,...
On te laisse finir les calculs, écris les nous stp pour que l'on puisse voir si tout est ok...courage et au plaisir de te lire !!!!!.............
Sur ta figure il est très facile de vérifier visuellement ton PS obtenu par le calcul, il suffit de prendre ta règle graduée :
- tu mesure IH
- on te donne IJ
- tu fais le produit des 2, c'est ça le Produit Scalaire des deux vecteurs !!!
Comme tu m'a dis que tu souhaitais absolument comprendre le produit scalaire (PS), et que tu ne semble pas bien maitriser l'outil (vu que tu commence !), je vais te donner quelques éléments :
b) toujours pareil, disposer devant soi d'une figure que tu construit la plus "précise et complète" possible (en fonction des données du sujet), c'est la base !, et savoir son cours :
-------------------------------------------------------------------
le PS de 2 vecteurs est :
1 ) le produit des modules des 2 vecteurs par le cosinus de l'angle entre les vecteurs,
ou bien :
2) simplement le produit du module de l'un des vecteurs par le module du projeté orthogonal (sur la droite support du 1er vecteur) du second vecteur ! (reprendre le cours pour bien cerner visuellement la chose !!!)
------------------------------------------------------------------
Donc IJ.IK (le . veut dire Produit scalaire) =
avec 1)
IJ.IK = IJ x IK x cos I = 16 x 10 x (53/80) = 106
(dans le a) tu auras calculé le cos I, entre autres)
(le x veut dire multiplié)
avec 2)
IJ.IK =106=IJ x IH
(H étant le projeté orthogonal de K sur IJ)
D'où IH = 106/16
puis avec Pythagore tu trouve la valeur de HK qui est la longueur de la hauteur issue de K,...
On te laisse finir les calculs, écris les nous stp pour que l'on puisse voir si tout est ok...courage et au plaisir de te lire !!!!!.............
Sur ta figure il est très facile de vérifier visuellement ton PS obtenu par le calcul, il suffit de prendre ta règle graduée :
- tu mesure IH
- on te donne IJ
- tu fais le produit des 2, c'est ça le Produit Scalaire des deux vecteurs !!!
formules
bonjour,
avec les notations
 =aire,
=aire,  demi-périmètre
demi-périmètre
loi des sinus

(se démontre en calculant l'aire avec une hauteur)
formule d'Al-Kashi

se démontre avec le produit scalaire
la restriction du cos() étant une bijection de sur
sur 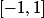 ,
,
au contraire du sinus
formule de Héron
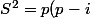(p-j)(p-k))
se démontre en substituant dans
dans

avec les notations
loi des sinus
(se démontre en calculant l'aire avec une hauteur)
formule d'Al-Kashi
se démontre avec le produit scalaire
la restriction du cos() étant une bijection de
au contraire du sinus
formule de Héron
se démontre en substituant
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
