pourriez-vous m'aidez svp
soit
posons
je cherche à démontrer que
que dois-je faire ?
merci
Une somme : comlexes
6 messages
- Page 1 sur 1
une somme : comlexes
par sue » 26 Nov 2006, 21:03
salut,
pourriez-vous m'aidez svp
soit
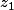
et 
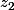
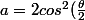les racines carrées de (-cos(\theta) + isin(\theta)))
et 
, 
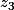
les racines carrées de
.
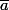
posons
je cherche à démontrer que
: 
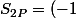et ^p 2^{p+2} (cos\theta/2)^{2p} cos(p\theta))
que dois-je faire ?
merci
pourriez-vous m'aidez svp
soit
posons
je cherche à démontrer que
que dois-je faire ?
merci
par tize » 26 Nov 2006, 22:22
Bonour,
dans l'hypothèse ou>0)
(sinon adapter...)
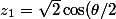e^{i\frac{\pi-\theta}{2}})
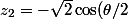e^{i\frac{\pi-\theta}{2}})
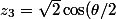e^{i\frac{\pi+\theta}{2}})
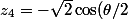e^{i\frac{\pi+\theta}{2}})
Il me semble qu'en élevant à la puissance n ça roule bien moyennant quelques petites formule trigo...
dans l'hypothèse ou
Il me semble qu'en élevant à la puissance n ça roule bien moyennant quelques petites formule trigo...
par sue » 26 Nov 2006, 23:07
en fait je trouve pareil c'est sur la suite que je bloque :hein:
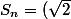je trouve^{n+2} i^{n+1} cos^n(\frac{\theta}{2}) sin(\frac{n\theta}{2}))
mais est_ce que cela est égale à 0 si n=2p ?! :hein:
je trouve
par tize » 27 Nov 2006, 21:17
Au passage j'avais oublié un + dans mon .
Sinon avec ce que j'ai donné hier, je trouve :
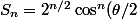\(e^{in\frac{\pi-\theta}{2}}\(1+(-1)^n\)+e^{in\frac{\pi+\theta}{2}}\(1+(-1)^n\)\))
et je trouve bien
, le reste se déduit simplement je crois...
Sinon avec ce que j'ai donné hier, je trouve :
et je trouve bien
par sue » 27 Nov 2006, 22:17
merci beaucoup Tize , je trouve pareil pour 
et du coup le résultat se déduit facilement :we:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :