Une petit pblm de DL
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 23:37
par Judoboy » 02 Mai 2012, 23:37
Dinozzo13 a écrit:Me revoilà pour une autre question :
On me demande d'écrire les DL d'ordre

en 0 de
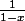
et
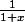
puis calculer le produit dans le but de montrer que :
)
.
J'ai donc
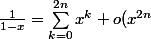=1+x+x^2+...+x^{2n} +o(x^{2n}))
et
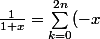^k +o(x^{2n})=1-x+x^2-...+x^{2n}+o(x^{2n}))
.
Mais le problème c'est le calcul du produit :
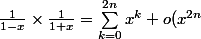\) \times \( \sum_{k=0}^{2n} (-x)^k +o(x^{2n}) \))
.
Je ne vois pas du tout comment retrouver le résultat voulu.
Merci d'avance pour votre aide :++:
C'est hautement contre-productif comme méthode pour trouver ton DL.
Enfin si tu veux vraiment faire comme ça, tu peux rassembler en un seul terme tous les termes qui contiennent
)
(parce que
)
* un truc fini =
)
). Tu vas également avoir énormément de termes qui vont s'annuler quand tu vas développer ton produit
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 03 Mai 2012, 00:05
par Dinozzo13 » 03 Mai 2012, 00:05
Oui, je suis d'accord, mais mon problème réside dans le fait qu'on a un produit de deux sommes.
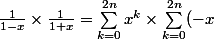^k)
.
J'ai remarqué que si on pose
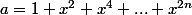
et
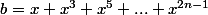
alors le produit vaut a²-b², mais bon, je ne sais pas si ça pars bien.
J'avais pensé à calculer calculer a et b mais bon...
vous l'aurez compris, je suis un peu perdu.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Mai 2012, 00:27
par Skullkid » 03 Mai 2012, 00:27
T'as oublié des termes là :
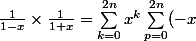^p + o(x^{2n})\sum_{k=0}^{2n} x^k + o(x^{2n})\sum_{p=0}^{2n}(-x)^p + o(x^{4n}))
Le premier terme est un produit de deux sommes, donc tu le développes (en une double somme) et tu le regardes dans le blanc des yeux, voir s'il n'y a pas moyen de le réécrire d'une façon plus proche du résultat que tu veux obtenir.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 03 Mai 2012, 00:37
par Dinozzo13 » 03 Mai 2012, 00:37
Skullkid a écrit:\sum_{k=0}^{2n} x^k + o(x^{2n})\sum_{p=0}^{2n}(-x)^p + o(x^{4n}))
oui, mais cette chose vaut
)
Je suis désolé, mais je ne comprends pas bien ce que tu veux que je fasse avec le produit
^p)
.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Mai 2012, 00:59
par Skullkid » 03 Mai 2012, 00:59
Dinozzo13 a écrit:oui, mais cette chose vaut
)
Certes, mais il faut quand même l'écrire. Le produit, tu le développes :
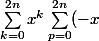^p = \sum_{k=0}^{2n}\sum_{p=0}^{2n} (-1)^p x^{p+k})
Là-dedans, y a pas mal de termes que tu peux jeter dans le petit o. Une fois que c'est fait, tu veux te ramener à quelque chose de la forme
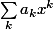
donc il faut réindexer.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 03 Mai 2012, 01:11
par Dinozzo13 » 03 Mai 2012, 01:11
Ah oui, tout ceux dont le deg est supérieur ou égal à 2n !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
en 0 de
et
puis calculer le produit dans le but de montrer que :
.
et
.
.
