Trouver la valeur de a d'une matrice.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 10 Mai 2023, 16:06
par novicemaths » 10 Mai 2023, 16:06
Bonjour
Là, je suis face à un petit casse tête, je dois trouver la valeur exact de a.

Est-ce que je dois utiliser le déterminant ?
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Mai 2023, 18:13
par GaBuZoMeu » 10 Mai 2023, 18:13
Bonjour,
Sans autre condition sur la matrice A, la valeur exacte est toujours 42.


Mais je parie que tu as oublié de nous dire ce qui est demandé à la matrice A !
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 10 Mai 2023, 18:43
par novicemaths » 10 Mai 2023, 18:43
Bonsoir
Image d'un plan (avec paramètres).
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Mai 2023, 22:28
par GaBuZoMeu » 10 Mai 2023, 22:28
Qu'est-ce que ça veut dire ? Tu n'es pas d'une clarté limpide, tu ferais beaucoup mieux de donner l'énoncé exact.
Je suppose que ça veut dire qu'on demande de trouver a tel que A soit de rang 2 ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 12 Mai 2023, 22:19
par novicemaths » 12 Mai 2023, 22:19
Bonsoir
Voici la question exact.
 = (4y+ax++2z, 5y+4x+z, 2y+4x+5z))
Pour quelle valeur du paramètre a l'application linéaire
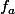
n'est pas isomorphe ?
Pour commencer, j'ai réalisé une matrice, pour trouver à avec le déterminant.
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 13 Mai 2023, 09:01
par GaBuZoMeu » 13 Mai 2023, 09:01
N'est pas un isomorphisme, je suppose ?
Pourquoi le

vient avant le

dans les formules ? Enfin, pas d'importance.
On peut bien sûr utiliser un déterminant, mais ce n'est pas obligatoire.
On peut partir de l'hypothèse que

, déterminer

et

à l'aide d'un système
et en déduire

.
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 14 Mai 2023, 16:53
par novicemaths » 14 Mai 2023, 16:53
Bonsoir
Voici le début de mon calcul, c'est incorrect.
Pourriez-vous s'il vous plait me dire ce que je dois rectifier ?
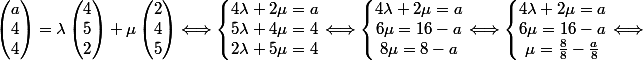
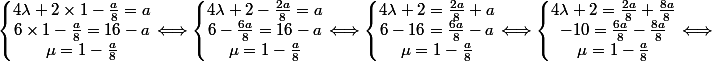
 \times (-8)}{2} \\ <br /> \mu = 1- \frac{a}{8}<br />\end{matrix}\right. \Longleftrightarrow)
Merci
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Mai 2023, 20:43
par GaBuZoMeu » 14 Mai 2023, 20:43
Les deux dernières équations dde ton système permettent de trouver

et

.
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 14 Mai 2023, 21:09
par novicemaths » 14 Mai 2023, 21:09
Là, je suis un peu perdu.
Est-ce qu'il faut que je trouve mu et lambda, est ensuite déterminé la valeur de a ?
A bientôt
-
GaBuZoMeu
- Habitué(e)
- Messages: 6146
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 15 Mai 2023, 09:31
par GaBuZoMeu » 15 Mai 2023, 09:31
C'est bien ce que je t'avais suggéré plus haut, non ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 16 Mai 2023, 18:03
par novicemaths » 16 Mai 2023, 18:03
Bonsoir
 \times (-8)}{2}\\ <br />\mu = 1 - \frac{a}{8}<br />\end{matrix}\right. \Longleftrightarrow \left\lbrace\begin{matrix}<br />4 \lambda + 2 = \frac{10 a}{8}\\ <br />a = \frac{80}{2}\\ <br />\mu = 1 - \frac{a}{8}<br />\end{matrix}\right. \Longleftrightarrow \left\lbrace\begin{matrix}<br />4 \lambda + 2 = \frac{10 \times 40}{8}\\ <br />a = 40\\ <br />\mu = 1 - \frac{40}{8}<br />\end{matrix}\right. \Longleftrightarrow \left\lbrace\begin{matrix}<br />4 \lambda + 2 = \frac{400}{8}\\ <br />a = 40\\ <br />\mu = 1 - \frac{40}{8}<br />\end{matrix}\right. \Longleftrightarrow)
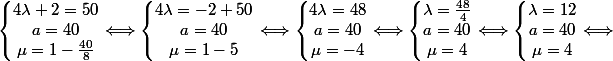
On a

et
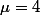
Là, je ne vois pas quoi faire ensuite.
A bientôt
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités

