Tribu des boréliens de IR = parties de IR ?

[Zapata]

Salut les gars,
je me posais la question suivante : est-ce que la tribu des boréliens de IR est égale à l'ensemble des parties de IR ?
Je me dis que non car si c'était le cas je le saurai... Mais c'est pas très rigoureux, et je ne suis pas du tout certain ! Auriez-vous un contre-exemple ?

[tize]

Effectivement, ça n'est pas la même chose...on peut construire grâce à l'axiome du choix une partie de R qui n'est pas mesurable, cela a déjà été fait dans le forum, fais une recherche tu trouveras facilement...

[ThSQ]

L'ensemble des boréliens de IR à le même cardinal que IR (la puissance du continu, la classe !) il y a donc beaucoup plus de parties de IR que de parties boréliennes.


Edit : je viens de lire la réponse de tize. l'AC est nécessaire pour montrer l'existence de partie non mesurable, mais il me semble qu'un argument de cardinal suffit pour les parties boréliennes.

[tize]

...je viens de lire la réponse de tize. l'AC est nécessaire pour montrer l'existence de partie non mesurable...

Oui c'est ce que je dis et effectivement la tribu borélienne de a la puissance du continu qui est bien "inférieure" à la puissance de

[Zapata]

Ah ok je savais pas du tout ! Dur dur d'imaginer une partie de IR qui ne soit pas un borélien !

[tize]

Oui, c'est pas facile à imaginer, j'ai retrouvé ce lien

[ThSQ]

la tribu borélienne de a la puissance du continu

Sans vouloir pinailler (bon, un peu quand même), la tribu borélienne de est de même cardinal que . Mais montrer que et sont équipotents nécessite à nouveau l'AC !

[ThSQ]

Ah ok je savais pas du tout ! Dur dur d'imaginer une partie de IR qui ne soit pas un borélien !

Facile, tu prends une partie de IR au hasard, il y a une probabilité de 1 qu'elle ne soit pas borélienne !

[tize]

Sans vouloir pinailler (bon, un peu quand même)...nécessite à nouveau l'AC !

Oui :we: tu as raison :ptdr:

Facile, tu prends une partie de IR au hasard, il y a une probabilité de 1 qu'elle ne soit pas borélienne !

Ca n'aide pas à l'imaginer, le hasard infini... (à mon tour de pinailler :we: ) mais ça donne une bonne idée de la proportion dans P(R)

[Zapata]

C'est dingue ce que vous dites !
En fait c'est chaque fois pareil en math, c'est toujours les éléments les plus nombreux les plus difficiles à "montrer". J'ai toujours du mal à expliquer aux gens qu'il y a bcp plus de transcendants que d'algébriques, mais que pourtant ils sont beaucoup plus difficile à trouver !
Ben en fait, je ne sais même pas ce qu'est l'axiome du choix, faudra que je remédie à ça !

[Lierre Aeripz]

Montrer que est équipotent à ne nécessite pas l'axiome du choix, pas même l'axiome du choix dénombrable. En effet a une structure connue, donc on peut faire des choix. Pour montrer l'équipotence de 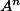et de A dans le cas général, il faut l'axiome du choix (je pense).
Plus généralement, la théorie des cardinaux nécessite l'axiome du choix (pour pouvoir dire que tout ensemble est équipotent à un ordinal et d'autres choses du genre).