Bonjour,

Désolé de n'avoir pas vue ces messages plutôt.
De même, merci l'aviateur et beagle d'y avoir prêté attention.
En effet, je trouve que ma démonstration laisse à désirer(car trop d'intuition à mon goût).
aviateur a écrit: coc0 a écrit:Soit x' un élément tel que: x'
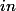
A\(B UC)
 <=> x'\in)
A, x'
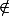
C et x'
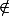
B
J'ai des questions à poser à @coco concernant la rigueur de la démonstration:
qu'est ce qui est équivalent à
 ])
?
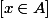
ou bien
[
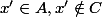
et
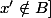
D'autre part comment faut-il lire cette dernière assertion? En particulier qu'elle est la signification de la virgule?
Finalement, le lecteur attentif remarquera que l'affirmation de cette équivalence semble un peu rapide vu le contexte de la question et la façon dont est rédigé l'ensemble.
Je souhaitais dire que:
 <=> x' \in A,x' \notin C et x'\notin B)
De plus, j'ai introduit x' (et pas introduit deux fois x) car je pars de l'hypothèse que je ne sais pas que
(A\(BUC) = (A\B)\C.
Si j'aurais écrit:
\backslash C)
<=>... et
)
...
(en gros deux fois x ), je trouve que que l'on considère de base que (A\(BUC) = (A\B)\C.
En revanche, x' me chiffonne après. En effet, bien qu’extrêmement intuitif, quand j'arrive à:
\backslashC <=> x\in A\backslash(BUC))
. j'enlève x' sans justification et c'est cela qui me dérange un peu.
beagle a écrit:bah tout dépend si l'objectif c'est de partir du cours, genre:
"La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie que « non(A et B) » est identique à « (non A) ou (non B) ».
La négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que « non(A ou B) » est identique à « (non A) et (non B) ».
et on veut voir des trucs comme ça dans la rédaction ...
ou alors si on regarde juste les patates et là les trucs disent bien je veux du A qui n'est pas B et qui n'est pas C,
ils le disent à leur manière, juste la séquence n'est pas la même.
Donc quand on est prof et qu'on veut des réponses qui sont en relation avec du cours,
comment on rédige pour que justement le gars te dise pas,
ben A sans B et sans C quoi!
En effet, je sais que je peux faire :
= A\cap{}\bar{(B\cup{}C)}= A\cap(\bar{B} \cap \bar {C})=A \cap \bar{B} \cap \bar{ C}=(A\backslash{B} )\backslash C)
.
Mais, en faisant l'exercice, j'ai trouvé intéressant de faire par des ''patates''

aviateur a écrit:Bonjour
Oui et non: il y a bien des patates, là je suis d'accord. Mais simplement elles ne sont pas très bonnes. Ce n'est pas le point de vue d'un prof mais plutôt d'un mathématicien.
On devine que la démonstration qu'il a vu c'est surement utiliser la définition de
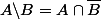
Pour le rassurer on peut lui dire que l'idée de sa démonstration est bonne, mais, par contre, le laisser partir avec une telle rédaction ça laisse à désirer.
beagle a écrit:Pour le B union C :
x n'appartient pas à B ou C est x n'appartient pas a B et x n'appartient pas à C
Pour le (A\B)\C
n'appartient pas à C, puis n'appartient pas à B
un peu de décoration issu du cours et cela le fait
manque quelques lignes
Si je puis me permettre, comment auriez vous rédigé, avec la même idée, cette démonstration.
Merci
coc0

