On pourrait discuter longtemps des jugements de valeur de Dieudonné sur ceci ou cela. Jugements qu'il est souvent seul à partager. Il est particulièrement agressif sur une fonction multiforme qu'on utilise tous : l'argument d'un complexe. "Il est insensé de mesurer les angles" répètait-il à tout va. "La trigo ne sert à rien". Et autres affirmations à l'emporte-pièce qui n'ont de sens que dans un univers trés particulier : les hautes sphères où il volait.
Pour le reste, je crois avoir dit que les surfaces de Riemann uniformisaient les fonctions multiformes.
X^x
30 messages
- Page 2 sur 2 - 1, 2
D'accord il était souvent assez catégorique mais dans le cas qui nous préocuppe on peut penser qu'il avait raison.
Je pense réellement que se limiter à x > 0 pour toute manipulation de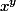 est une attitude assez prudente, et qui évite beaucoup de soucis.
est une attitude assez prudente, et qui évite beaucoup de soucis.
Voici un autre exemple problématique: sur et la fonction
et la fonction  = z^2 -1) . Il n'existe aucune fonction holomorphe
. Il n'existe aucune fonction holomorphe  sur
sur  telle que
telle que  et pourtant il existe
et pourtant il existe  holomorphe sur
holomorphe sur  telle que
telle que  .
.
Autrement dit dans ce cas, la racine carrée c'est pas l'exp du Log puissance 1/2. Aie ! Ca pique non ?
Je pense réellement que se limiter à x > 0 pour toute manipulation de
Voici un autre exemple problématique: sur
Autrement dit dans ce cas, la racine carrée c'est pas l'exp du Log puissance 1/2. Aie ! Ca pique non ?
yos a écrit:Ce que je voulais dire surtout, c'est que si on demande l'ensemble de définition de la fonction x^x, on s'expose à des problèmes : une réponse genre "c'est R*+ car c'est égal à exp(xlnx)" n'est pas du tout satisfaisante ou bien il faut retourner au collège ou on apprend le sens de (-2)^(-2).
Mouais, si elle était prolongeable sans problèmes, les mathématiciens l'aurait déjà prolongé. La question posée au départ du sujet n'est pas clairement posée, on est d'accord. Il me semblait que exp(xlnx) était une indication.
Je ne comprend pas pourquoi Yos s'en prend a ma réponse comme cela. Il faut que je retourne au collège apprendre le sens de (-2)^(-2)?
Ok, no pb. Apres tout, des forums de math, il y en a plein. J'en trouvrai bien un sur lequel on peut discuter sans être obliger de jouer à "c'est moi le plus fort".
Astalavista.
Je ne comprend pas pourquoi Yos s'en prend a ma réponse comme cela. Il faut que je retourne au collège apprendre le sens de (-2)^(-2)?
Ok, no pb. Apres tout, des forums de math, il y en a plein. J'en trouvrai bien un sur lequel on peut discuter sans être obliger de jouer à "c'est moi le plus fort".
Je ne m'adressais pas à quelqu'un en particulier et en tout cas pas à toi : je viens seulement de voir que tu avais écrit ça. Je tentais plutôt de répondre à Nicolas en me contorsionnant pour récupérer ce qui était récupérable dans mes idées. Je suis désolé que tu le prennes ainsi. En tout cas je ne mérite pas que tu t'en ailles.
Je reviens au sens de ma phrase avec un autre exemple. Quand on demande l'ensemble de définition de ln[(x-1)/(x+1)], on ne dit pas :
"c'est ]1, +oo[ car ln[(x-1)/(x+1)]=ln(x-1)-ln(x+1)".
Ici c'est pareil.
L'auteur de la question proposait un ensemble de définition et je lui ai confirmé que c'est valable. Cela dit, je suis bien d'accord que l'on doit se restreindre à R+ pour que ce soit intéressant.
J'ai mis au propre mes quelques (modestes) idées.
(EDIT: j'ai corrigé ce message, dont la version initiale parlait de - avec
avec  , alors que le signe de
, alors que le signe de  importe finalement peu.)
importe finalement peu.)
Remarque.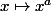 peut se définir :
peut se définir :
- si est irrationnel ou rationnel
est irrationnel ou rationnel 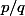 avec
avec  et
et  premiers entre eux et
premiers entre eux et  pair, uniquement sur
pair, uniquement sur 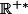 , par
, par 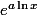
- si est rationnel
est rationnel 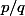 avec
avec  et
et  premiers entre eux et
premiers entre eux et  impair, sur
impair, sur 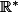 , par
, par =(x^p)^{1/q})
En d'autres termes, on ne peut définir facilement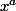 sur les
sur les  négatifs que si
négatifs que si  est rationnel
est rationnel 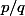 avec
avec  et
et  premiers entre eux et
premiers entre eux et  impair.
impair.
Remarque. Les rationnels à dénominateur impair étant denses dans , on serait tenté de définir
, on serait tenté de définir  pour
pour  réel
réel  :
:
^{-\beta}=\lim_{n\to +\infty}\left(-\frac{p_n}{q_n}\right)^{-p_n/q_n})
avec_n) une suite de rationnels à dénominateur impair tendant vers
une suite de rationnels à dénominateur impair tendant vers  , avec
, avec  et
et 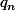 entiers naturels positifs et premiers entre eux.
entiers naturels positifs et premiers entre eux.
Il reste encore une petite...
Conjecture. Soit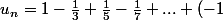^n\frac{1}{2n+1}\to\frac{\pi}{4})
On note avec
avec  et
et  et
et 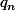 premiers entre eux.
premiers entre eux.
On sait que les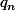 sont impair.
sont impair.
On conjecture que les sont impairs et les
sont impairs et les  sont pairs.
sont pairs.
Sauf erreur !
Nicolas
(EDIT: j'ai corrigé ce message, dont la version initiale parlait de -
Remarque.
- si
- si
En d'autres termes, on ne peut définir facilement
Remarque. Les rationnels à dénominateur impair étant denses dans
avec
Il reste encore une petite...
Conjecture. Soit
On note
On sait que les
On conjecture que les
Sauf erreur !
Nicolas
A propos de la fin de ton message. Le numérateur de la série harmonique alternée est clairement de parité alternée : Au dénominateur tu as le produit des entiers impairs donc pas de simplification par 2 possible, donc la parité de  avant ou après simplification de la fraction est la même. Au numérateur tu as une somme de nombres impairs (éventuellement négatifs) donc le résultat a la même parité que le nombre de termes de la somme.
avant ou après simplification de la fraction est la même. Au numérateur tu as une somme de nombres impairs (éventuellement négatifs) donc le résultat a la même parité que le nombre de termes de la somme.
30 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
