X^x
30 messages
- Page 1 sur 2 - 1, 2
x^x
est-ce que quelqu'un peut me confirmer ce qui suit?
le domaine de définition de X^X = x si x appartient à R*+.
p/q <0 tel que p^q=1 et q= 2n+1.
est qu'elle la dérivé de la fonction précédente. avec preuve si possible.
le domaine de définition de X^X = x si x appartient à R*+.
p/q <0 tel que p^q=1 et q= 2n+1.
est qu'elle la dérivé de la fonction précédente. avec preuve si possible.
memphisto a écrit:c'est bien de la fonctiondont vous parlez?
Parce qu'il me semble que cette fonction n'est pas définie sur les réels négatifs:, qui n'est définie que pour les réels positifs.
Cependant elle se prolonge par continuité en 0 par la valeur 1, qui est la limite en 0 de.
Allons allons!
Tu as le droit de faire
Car une racine (2n+1)ème est définie sur R.
On a le droit d'écrire ^{-\frac{8}{17}}) uniquement car on a une fraction négative à dénominateur impair en exposant (voir ci-dessous).
uniquement car on a une fraction négative à dénominateur impair en exposant (voir ci-dessous).
En revanche, on ne peut pas écrire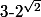 (EDIT)
(EDIT)
Selon moi :
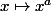 peut se définir :
peut se définir :
- si est irrationnel ou rationnel
est irrationnel ou rationnel 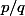 avec
avec  et
et  premiers entre eux et
premiers entre eux et  pair, uniquement sur
pair, uniquement sur 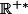 , par
, par 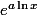
- si est rationnel
est rationnel 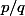 avec
avec  et
et  premiers entre eux et
premiers entre eux et  impair, sur
impair, sur 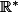 , par
, par =(x^p)^{1/q})
Donc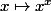 n'est pas définie sur tout
n'est pas définie sur tout 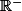
Sauf si on l'autorise à prendre des valeurs complexes. (EDIT)
Sauf erreur.
Nicolas
En revanche, on ne peut pas écrire
Selon moi :
- si
- si
Donc
Sauf si on l'autorise à prendre des valeurs complexes. (EDIT)
Sauf erreur.
Nicolas
Par exemple, on sait que :

Soit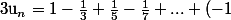^{n}\frac{1}{2n+1})
La suite_n) est une suite de rationnels tendant vers l'irrationnel
est une suite de rationnels tendant vers l'irrationnel  .
.
On conjecture que tous ses dénominateurs (après simplification) sont impairs.
Donc on pourrait utiliser_n) pour définir
pour définir ^{\frac{\pi}{4}})
Or :
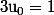
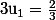 => numérateur pair
=> numérateur pair
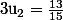 => numérateur impair
=> numérateur impair
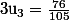 => numérateur pair
=> numérateur pair
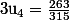 => numérateur impair
=> numérateur impair
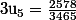 => numérateur pair
=> numérateur pair
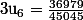 => numérateur impair
=> numérateur impair
On conjecture que cette alternance de parité du numérateur continue ainsi à l'infini.
Dans ce cas^{u_n}) prend alternativement les valeurs -1 et +1, et ne converge pas.
prend alternativement les valeurs -1 et +1, et ne converge pas.
Nicolas
Soit
La suite
On conjecture que tous ses dénominateurs (après simplification) sont impairs.
Donc on pourrait utiliser
Or :
On conjecture que cette alternance de parité du numérateur continue ainsi à l'infini.
Dans ce cas
Nicolas
Vouloir donner un sens dans certains cas à 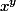 quand x n'est pas strictement positif conduit à une pléthore de cas particuliers assez gênants, car les règles de calcul usuelles s'appliquent mal comme on l'a vu plus haut avec les exemples de Nicolas_75.
quand x n'est pas strictement positif conduit à une pléthore de cas particuliers assez gênants, car les règles de calcul usuelles s'appliquent mal comme on l'a vu plus haut avec les exemples de Nicolas_75.
Mieux vaut en rester à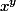 défini que pour x >0.
défini que pour x >0.
D'autre part passer par une détermination dans n'est pas souhaitable non plus: les mathématiciens s'accordent pour dire que
n'est pas souhaitable non plus: les mathématiciens s'accordent pour dire que 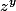 n'est pas définissable de façon satisfaisante.
n'est pas définissable de façon satisfaisante.
Mieux vaut en rester à
D'autre part passer par une détermination dans
1) Je ne vois pas pourquoi tu parles de conjecture : quand on multiplies des nombres impairs, on obtient un nombre impair.
2) Pourquoi ça ne convergerait pas?
3) Quand tu prends (pour p>0, q>0),^{-\frac{p}{q}}) , tu as simplement
, tu as simplement ^{-\frac{p}{q}}) .
.
D'où mon prolongement "naturel" pour x réel <0 :^x) .
.
4) Je pense que ta suite converge vers^{-\frac{\pi}{4}}) .
.
2) Pourquoi ça ne convergerait pas?
3) Quand tu prends (pour p>0, q>0),
D'où mon prolongement "naturel" pour x réel <0 :
4) Je pense que ta suite converge vers
Je vois ce dis Nicolas75. Il y a en effet un problème avec la suite Un^Un que je n'avais pas vu. A un moment tu as parlé de dénominateur impair alors qu'il s'agissait de numérateur impair je pense, et c'est peut-être ce que je n'avais pas compris. Tu es bien d'accord que (-p/q)^(-p/q) a un sens quand q est impair (p, q positifs) : tu le calcules toi-même dans le précédent message. Je pense que tu es d'accord aussi que les rationnels de ce type sont denses dans R , même si on impose à p d'être lui aussi impair. Du coup, tu as x^x qui est bien défini pour une classe dense et qui coïncide avec -(-x)^x. D'où le prolongement On obtient un truc genre e^{x\ln|x|}) (pas continu en 0).
(pas continu en 0).
C'est sans intérêt je le reconnais, d'autant plus que vue ta remarque pertinente, cela ne coïncide pas avec les valeurs espérées de (-p/q)^(-p/q) quand p est pair.
Ce que je voulais dire surtout, c'est que si on demande l'ensemble de définition de la fonction x^x, on s'expose à des problèmes : une réponse genre "c'est R*+ car c'est égal à exp(xlnx)" n'est pas du tout satisfaisante ou bien il faut retourner au collège ou on apprend le sens de (-2)^(-2).
Pour terminer,
je réponds à la remarque d'El Gato qui porte un jugement de valeur bien péremptoire sur les fonctions multiformes et leurs déterminations complexes, qui sont d'usage constant en math. L'invention par Riemann des surfaces qui portent son nom ont parfaitement permis de travailler avec ces fonctions.
C'est sans intérêt je le reconnais, d'autant plus que vue ta remarque pertinente, cela ne coïncide pas avec les valeurs espérées de (-p/q)^(-p/q) quand p est pair.
Ce que je voulais dire surtout, c'est que si on demande l'ensemble de définition de la fonction x^x, on s'expose à des problèmes : une réponse genre "c'est R*+ car c'est égal à exp(xlnx)" n'est pas du tout satisfaisante ou bien il faut retourner au collège ou on apprend le sens de (-2)^(-2).
Pour terminer,
je réponds à la remarque d'El Gato qui porte un jugement de valeur bien péremptoire sur les fonctions multiformes et leurs déterminations complexes, qui sont d'usage constant en math. L'invention par Riemann des surfaces qui portent son nom ont parfaitement permis de travailler avec ces fonctions.
yos a écrit:Pour terminer,
je réponds à la remarque d'El Gato qui porte un jugement de valeur bien péremptoire sur les fonctions multiformes et leurs déterminations complexes, qui sont d'usage constant en math. L'invention par Riemann des surfaces qui portent son nom ont parfaitement permis de travailler avec ces fonctions.
Non. Les fonctions multiformes ne sont plus utilisées en math pures depuis longtemps. Pour cela, consulter l'introduction du chapitre 9 du tome 1 des "Elements d'Analyse" de J. Dieudonné (chapitre intitulé: "fonctions analytiques"), qui contient en outre une interessante discussion sur le caractère parfaitement inepte d'une définition de
On peut parfaitement manipuler des fonctions holomorphes f telles que
La théorie des surfaces de Riemann contient justement la solution à toutes les impasses des fonctions dites "multiformes". Cette théorie permet de se passer de telles "fonctions".
Fondamentalement, dans le plan complexe, la possibilité d'inverser "dépend de la forme" de l'ouvert sur lequel est défini une fonction.
Le cas des ouverts simplement connexes ne pose pas de problème. Mais dès que l'ouvert n'est plus simplement connexe, des phénomènes étranges se produisent: une fonction peut avoir une racine carrée sans avoir de Log etc.
Une solution correcte à ces problèmes passe par des outils de topologie différentielle, et non pas par des "fonctions multiformes", dont la définition contredit la notion même d'application, et qui a le principal défaut de conduire aux problèmes évoqués par Nicolas_75, plus bien d'autres encore.
En d'autres termes: on n'inverse pas facilement dans un revêtement à une infinité de feuillets.
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Ben314 et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
